×

Warning

Please Login to Read More...

Angle of Elevation

Angle of Elevation

An angle of elevation is the angle between the line of sight (an imaginary line from an observer's eye to a perceived object) and the horizontal when an observer looks upward. Suppose that from a point O, the person looks up at a hot air balloon B, placed above the level of his eye. The angle which the line of sight makes with the horizontal through O is called the angle of elevation of hot air balloon B.

Note: i) The elevation angle is some times called as altitude angle.
        ii) Zenith angle = 90° – elevation angle

Example
Real life example
Practical scenario - I

Different practical conditions are illustrated below along with relevant formulae.

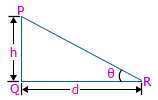
(i). Say, the angle of elevation of a tower from a distance 'd' from its foot is 'θ' and height of the tower is 'h' meter(refer ΔPQR). Then
       

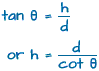
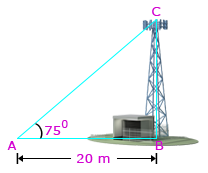
  • Example: A cell tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 75°. Find the height of the tower.
    Sol: Let height of the tower is BC.
    Distance between foot of the tower and the observation point is AB.
    From ΔABC, tan 75° = BC/AB
    2 + √3 = BC/20
    BC = 20(2 + √3)
    ∴ Height of the cell tower = 20(2 + √3) m.
Real life example
Practical scenario - II

(ii). Say, the angle of elevation of the top of a tower as observed from a point on the ground is θ1 and on moving 'd' meters towards the tower, the angle of elevation is θ2. Then the height of the tower h is given by
       

  • Example: The angle of elevation of the top of a tower from a certain point is 60°. If the observer moves 30 m towards the tower, the angle of elevation of the top of the tower increases by 15°. What is the height of the tower ?

Solution