Example
Q
As observed from the top of a 100 meters high lighthouse from the sea-level, the angles of depression of two ships are 30° and 60°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Sol:
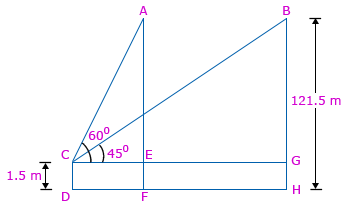
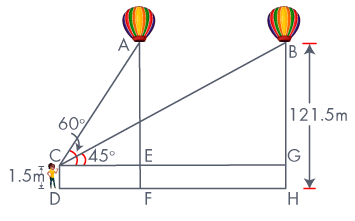
| In ΔACE, |
| tan 60° = AE/CE |
| √3 = (AF – EF)/CE |
| √3 = (121.5 – 1.5)/CE |
| CE = 120/√3 m ---- (i) |
| In ΔBCG, |
| tan 45° = BG/CG |
| 1 = BG/CG |
| BG = CG |
| BG = CE + EG |
| EG = BG – CE |
| EG = (BH – GH) – CE |
| EG = (121.5 – 1.5) – (120/√3) (∵ from eq. (i)) |
| EG = 120 – (120/√3) |
| EG = 120((√3 – 1)/√3) meters |
| ∴ The distance traveled by balloon is 120((√3 – 1)/√3) meters. |