| Comparison of fractions with like denominators |
| • If two fractions have the like [i.e., same] denominator, then the fraction with greater numerator is greater. |
• Thus,  as 2 > 1. |
| Comparison of fractions with like numerators |
| • If two fractions have the like [i.e., same] numerator, then the fraction with greater denominator is smaller. |
• Thus,  as 19 > 17. |
| Comparison of fractions with unlike numerators and unlike denominators |
| In this comparison, we have two methods: (i) by making denominators equal and (ii) by making numerators equal. |
| By making denominators equal |
| • Find the L.C.M. of denominators of given unlike fractions. |
| • Convert the given unlike fractions into equivalent like fractions with the L.C.M. as common denominator. |
| • Compare the like fractions so obtained. |
| By making numerators equal |
| • Find the L.C.M. of numerators of given unlike fractions. |
| • Convert the given unlike fractions into equivalent like fractions with the L.C.M. as common numerator. |
| • Compare the like fractions so obtained. |
| Addition (or) Subtraction of like fractions |
| • For addition (or) subtraction of like fractions, numerators are added (or) subtracted while the denominator remains the same. |
• Eg:  . |
| Addition (or) Subtraction of unlike fractions |
| • Find the L.C.M. of denominators of given unlike fractions. |
| • Convert the given unlike fractions into equivalent like fractions with the L.C.M. as common denominator. |
| • Add (or) Subtract the like fractions so obtained. |
| Multiplication of fractions |
•  |
| • If there is a common factor in one of the numerators and one of the denominators, it may be removed by canceling before multiplying. |
| Reciprocal of a non-zero fraction |
• Reciprocal of any fraction  such that the product of these two fractions is equal to 1, i.e.,  . |
| Division of fractions |
| • In order to divide a fraction by another fraction, we multiply the dividend by the reciprocal of the divisor. |
• If  are two fractions then the division of these two fractions given as
 . |
Fractions: A fraction is a part of a whole. Mathematically, we define fractions as the numbers of the form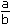 
, where a and b are whole numbers and b ≠ 0.
Therefore, a fraction consists of a top number and bottom number, separated by a dividing line. The top number is called the numerator and bottom number is called the denominator. For example, consider the fraction 
. In this fraction, '5' is called the numerator and '13' is called the denominator.
Types of fractions: Following are the different types of fractions:
- Proper fraction: A fraction whose numerator is less than its denominator, is called a proper fraction. For example: is a proper fraction where numerator is less than its denominator.
- Improper fraction: A fraction whose numerator is greater than (or) equal to its denominator, is called an improper fraction. For example:
is an improper fraction where numerator is greater than its denominator and similarly, 
is an improper fraction where numerator is equal to its denominator.
- Eg: Convert
into an improper fraction.
Sol: 
- Simple fraction: A fraction both of whose numerator and denominator [i.e., terms] are whole numbers, is called a simple fraction. Example:
.
- Complex fraction: A fraction whose one or both the terms are fractions, is called a complex fraction. Examples for complex fractions are:
, ............, etc.
- Vulgar fraction: A fraction whose denominator is a whole number other than 10, 100, 1000 . . . etc, is called a vulgar fraction. Example:
, .........., etc.
- Mixed fraction: A fraction which can be expressed as a sum of a natural number and a fraction is called a mixed fraction.Example:
.
- Equivalent fractions: Fractions having the same value are known as equivalent fractions. An equivalent fraction of a given fraction can be obtained by multiplying (or) dividing its numerator and denominator by the same non-zero number. Thus,
Clearly, 
are equivalent fractions.
- Eg: An equivalent fraction of
with numerator 18 is
Sol:
- Like fractions: Fractions having the same denominator are called like fractions. For example:
are like fractions because their denominators are same.
Example: Add the given like fractions 
Sol: 
- Unlike fractions: The fractions having different denominators are called unlike fractions. For example:
are unlike fractions because denominators of the fractions are not same.
- Unit fractions: The fractions with 1 as numerator are known as unit fractions. For example:
are unit fractions because their numerator is '1'.
Fractions In Lowest Terms (or) In Simplest Form: A fraction is said to be in lowest terms (or) in simplest form if the H.C.F. of its numerator and denominator is 1. For example: the fraction 
is in simplest form because H.C.F. of 2 and 3 is 1. In order to reduce a fraction to its lowest terms, divide each term by their H.C.F.
Simplification: In order to simplify a given expression involving fractions, we use the following rules: Use of BODMAS rule and Removal of brackets.
- Use of BODMAS rule: We simplify the expressions by applying the operations strictly in the order (1) Bracket (2) Of (3) Division (4) Multiplication (5) Addition (6) Subtraction.
- Removal of brackets: We strictly remove the different types of brackets in the following order: (1) Bar or Vinculum (–) (2) Parenthesis () (3) Curly brackets {} (4) Square brackets [].
