An Arab sheikh had 29 horses in his stable. After his death, it was known through his will that he
wanted them to be distributed as - half to his wife, one-sixth to his elder son, one fifth to his
younger son and one tenth to the jockey. The family members were perplexed as how to divide the odd
number horses into half. Their neighbor, a mathematics scholar, intervened saying he would take up
the
job. He added one of his own horses making the number thirty. Then he distributed  to the
sheikh's
wife
(i.e., 15),
to the
sheikh's
wife
(i.e., 15), 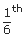 to
the elder son (i.e., 5),
to
the elder son (i.e., 5), 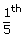 to the younger son (i.e., 6) and
to the younger son (i.e., 6) and 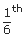 to the jockey
(i.e., 3). All
these added up to 29 and he took back his own horse. How did he manage and where is the flaw ?
to the jockey
(i.e., 3). All
these added up to 29 and he took back his own horse. How did he manage and where is the flaw ?

 and
fulfilled the sheikh's desire. The sheikh, himself, was either poor in math or wily!
and
fulfilled the sheikh's desire. The sheikh, himself, was either poor in math or wily!