Vector equation of the plane – Normal form
The vector equation of the plane which is at a distance of 'p' from the origin along the unit vector n is r . n = p.
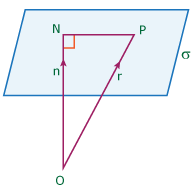
Proof:
Let the perpendicular from the origin 'O' to the plane meet at ' N '.
Then ON = pn
Let P be any point in the plane and OP = r
∴ ON ⊥ NP
| ⇒ | ON . NP = 0 |
| ⇒ | ON . (OP – ON) = 0 |
| ⇒ | pn . (r – pn) = 0 |
| ⇒ | (r . n) – p (n . n) = 0 (∵ r . n = n . r) |
| ⇒ | (r . n) – p = 0 (∵ n . n = 1) |
| ⇒ | (r . n) = p |