Vector area of a parallelogram
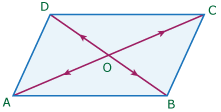
If ABCD is a parallelogram, then its vector area
in terms of the diagonals AC and BD is
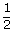 ( AC × BD )
( AC × BD )
Proof:
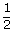 (AC × BD) (AC × BD) |
= | 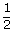 (AB +
BC) × (BA + AD) (AB +
BC) × (BA + AD) |
| = | 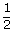 [AB ×
BA + AB ×AD + BC × BA + BC
× AD] [AB ×
BA + AB ×AD + BC × BA + BC
× AD]
|
|
| = | 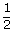 [AB ×
AD + (–CB) × BA] [AB ×
AD + (–CB) × BA]
|
|
| = | 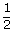 [AB ×
AD + (–CB) × CD] (∵ BA
= CD) [AB ×
AD + (–CB) × CD] (∵ BA
= CD)
|
|
| = | 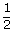 (AB × AD) + (AB × AD) + 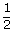 (CD × CB) (CD × CB) |
|
| = | vector area of Δ ABD + vector area of Δ CDB | |
| = | vector area of ABCD. |