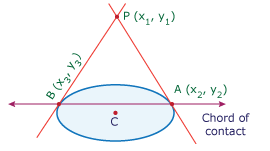
If P(x1, y1) is an external point to the ellipse S = 0, then the equation of the chord of contact to P is S1 = 0.
Let the tangents through P(x1, y1) to the given ellipse S = 0 touch the ellipse at A(x2, y2) and B(x3, y3).
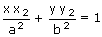
passes through P(x1, y1)
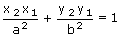 ...... (1)
...... (1)Similarly since P lies on the tangent at B is
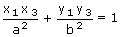 ...... (2)
...... (2)
From (1) and (2) points A(x2, y2), B(x3, y3)
satisfy the equation S ≡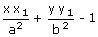 = 0
= 0
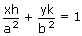 and it passes through the point (x1, y1) we have
and it passes through the point (x1, y1) we have
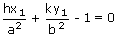
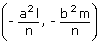 .
.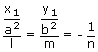
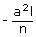 ,
y1 =
,
y1 = 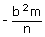
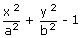 = 0
= 0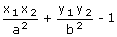 = 0
= 0
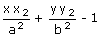 =
0 passes through P(x1/>, y1).
=
0 passes through P(x1/>, y1).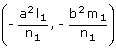
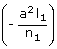 + m2
+ m2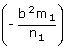 +
n2 = 0
+
n2 = 0