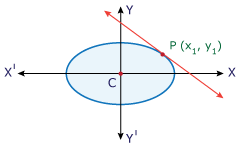
The equation of the chord joining two points (x1, y1) and (x2, y2) on the ellipse S = 0 is S1 + S2 = S12.
Let P(x1, y1) and Q(x2, y2) be
two points on the ellipse 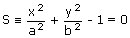 , then S11 = 0 and S22 = 0.
, then S11 = 0 and S22 = 0.
Substituting (x1, y1) it becomes S11 + S12 = S12
∴ (x1, y1) satisfy the equation S1 + S2 = S12.
∴ Equation of the chord PQ will be S1 + S2 = S12.
The condition for a straight line y = mx + c to be a tangent to the
ellipse 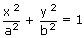 is
c2 = a2m2 +
b2.
is
c2 = a2m2 +
b2.
Given, y = mx + c ----- (i) and
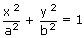 -----(ii)
-----(ii)
Substituting (i) in (ii), we get
The line will touch the ellipse iff the two points are coincident.
⇔ 4a4 c2m2 – 4(a2m2 + b2) a2 (c2 – b2) = 0
⇔ c = ± 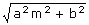
The equation of the tangent to the ellipse S = 0 at P(x1, y1) is S1 = 0.
By Theorem - I the equation of the chord PQ is S1 + S2 = S12 ...... (1)
Therefore the equation of the tangent at P obtained by taking limits as (x2, y2) tends to (x1, y1) on either side of (1)
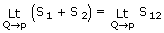
i.e., 2S1 = 0
Two tangents can be drawn to an ellipse from an external point.
Let the equation of the ellipse be S = 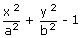 = 0.
= 0.
Then S11 > 0 ⇒ 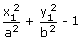 > 0
> 0
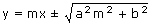 be
a tangent to the ellipse.
be
a tangent to the ellipse.
If it passes through P, then y1 = mx1 ± 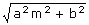
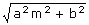
⇒ (x12 – a2)m2 = 2x1y1m + (y12 – b2) = 0
Discriminant of (i) is (2x1y1)2 – 4(x12 – a2)(y12 – b2)
= 4(b2x12 + a2y12 – a2b2)
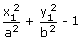 ) > 0
) > 0
∴ The two values of m are real and different.
The equation of the normal to the ellipse S = 0 at P(x1,
y1) is 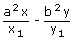 = a2 – b2 where
x1 ≠ 0 and y1 ≠ 0.
= a2 – b2 where
x1 ≠ 0 and y1 ≠ 0.
By the Theorem - III, the equation of the tangent to the ellipse S = 0 at P(x1, y1) is
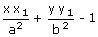 = 0.
= 0.
∴ Slope of the tangent at P = 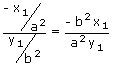
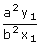
Hence the equation of the normal at P(x1, y1) is (y –
y1) = 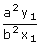 (x –
x1)
(x –
x1)
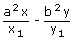 = a2 – b2.
= a2 – b2.At most four normals can be drawn from a given point to an ellipse.
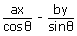 =
a2 – b2.
=
a2 – b2.
If this passes through the point (x1, y1) then 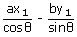 = a2
– b2 ...... (1)
= a2
– b2 ...... (1)
Equation (1) can be written as
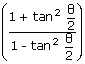 –
by1
–
by1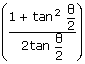 = a2 –
b2.
= a2 –
b2. After simplification we get
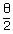 + 2
(ax1
+ a2e2) tan3
+ 2
(ax1
+ a2e2) tan3 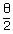 + 2 (ax1
– a2e2) tan
+ 2 (ax1
– a2e2) tan 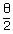 –
by1 = 0.
–
by1 = 0.
This, being a fourth degree equation, gives four values for tan 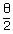 .
.
If we consider
one of the value as α1, tan 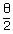 =
α1, θ = 2 Tan– 1 (α1) and the
general value of θ = 2nπ + 2 Tan– 1 (α1), which
gives the same point on the ellipse as θ
=
α1, θ = 2 Tan– 1 (α1) and the
general value of θ = 2nπ + 2 Tan– 1 (α1), which
gives the same point on the ellipse as θ
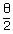 , we get on a point
on the ellipse, real or imaginary.
, we get on a point
on the ellipse, real or imaginary. Hence there will be at most four normals to the ellipse from a point.