i) 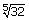 ii)
ii) 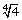 iii)
iii) 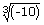 iv)
iv) 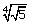 v)
v) 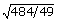 vi) √π
vi) √π
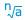 to be a surd:
to be a surd:- 'n' should be a positive integer greater than 1
- 'a' should be a positive rational number
-
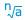 should be an irrational number
should be an irrational number
i) 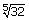
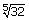 =
(32)1/5 =
(25)1/5 = 2
→ a rational number.
=
(32)1/5 =
(25)1/5 = 2
→ a rational number.
Condition 'c' is not satisfied.
So 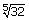 is
not a surd.
is
not a surd.
ii)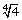
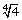 =
(4)1/4 = (22)1/4 = 21/2 = √2 →
irrational number.
=
(4)1/4 = (22)1/4 = 21/2 = √2 →
irrational number.
All three conditions are satisfied.
So 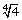 is a surd.
is a surd.
iii) 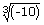
a = – 10 is not a positive rational number.
Condition 'b' is not satisfied.
So 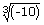 is not a surd.
is not a surd.
iv) 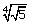
n = 4 but a = √5 is not a positive rational number.
So we may tend to conclude it as "not a surd".
But let us rewrite the term.
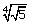 =
=
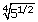 =
(51/2)1/4 = 51/8 =
=
(51/2)1/4 = 51/8 = 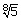
Now n = 8, a = 5 and 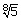 is an irrational number.
is an irrational number.
i.e, all the three conditions are satisfied.
So 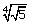 is a surd.
is a surd.
v)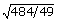
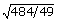 =
= 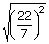 = 22/7
= 22/7
n = 2, a = 484/49 but √a = 22/7 which is a rational number.
Condition 'c' is not satisfied.
So 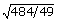 is not a surd.
is not a surd.
vi) √π
n = 2 and a = π
Since π is an irrational number, condition 'b' is not satisfied.
Hence √π is not a surd.