SURDS VS IRRATIONAL NUMBERS
Let us recall what is an irrational number and what is a surd.
Rational numbers can be expressed in the form
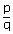 where p and q are integers.
where p and q are integers.
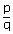 where p and q are integers.
where p and q are integers.
Rational numbers are non-terminating but have a recurring decimal part.
The numbers that can not be expressed in the form of 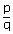 are
known as irrational numbers.
are
known as irrational numbers.
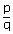 are
known as irrational numbers.
are
known as irrational numbers. When written as decimals, irrational
numbers neither terminate nor repeat.
When a positive rational number is not a power of 'n',
then the nth root of that number is irrational.
It is called as a surd.
Examples of irrational numbers that are not surds:
All non-terminating and non-repeating decimal numbers are irrational but not surds.
- 2.3154261587.....
- 3.1415926535... which is π(pi - ratio of circumference of a circle to its diameter)
- 2.7182818284... which is e(Euler's number)
- 1.6180339887... which is Φ(Golden ratio)
- 0.30102999566... which is log 2(logarithm of 2 to the base 10)
We can not express them as 
Therefore, all these are not surds.
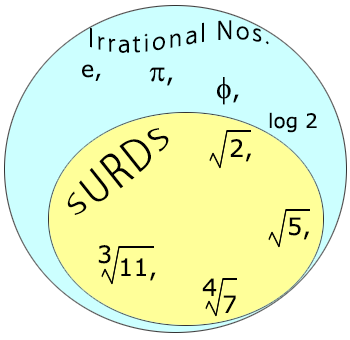
CONCLUSION :
All surds are irrational. But the converse is not true.
i.e, all irrational numbers are not surds.
This is represented by Venn diagrams in Set theory as: