The no. of ways of selecting one or more things from a group of 'n' different things is: 2n – 1
Proof:
The no. of ways of selecting some or all out of (p + q + r) things, where 'p' are alike of one kind, 'q' are alike of second kind and rest 'r' are alike of third kind is:
{(p + 1)(q + 1)(r + 1)} – 1
Proof:
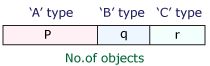
Total no. of ways where at least one object is selected = (p + 1) (q + 1) (r + 1) – 1
Total no. of ways of selecting one or more things from 'p' identical things of one kind, 'q' identical things of second kind, 'r' identical things of third kind from 'n' different things is:
{(p + 1)(q + 1)(r + 1).2n} – 1
Proof:
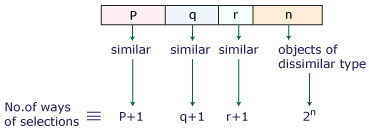
= (p + 1) (q + 1) (r + 1)2n – 1