Examples
Ex 1:
A ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall and its top reaches a window 6 m above the ground. Find the length of the ladder.
Sol:
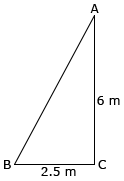
- Let AB be the ladder and CA be the wall with the window at A.
- BC = 2.5 m and CA = 6 m
- From Pythagoras theorem we have,
- ∴ The length of the ladder is 6.5 m.
| AB2 | = | BC2 + CA2 |
| = | (2.5)2 + (6)2 | |
| = | 42.25 | |
| AB | = | 6.5 |
Ex 2:
In ΔABC, if AD ⊥ BC, prove that AB2 + CD2 = BD2 + AC 2.
Sol:
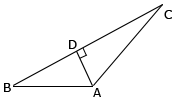
- From ΔADC, we have
- AC2 = AD2 + CD2 ----- (i) (by Pythagoras theorem)
- From ΔADB, we have
- AB2 = AD2 + BD2 ----- (ii) (by Pythagoras theorem)
- Subtracting (i) from (ii) , we have
- AB2 – AC2 = BD2 – CD2
- AB2 + CD2 = BD2 + AC2
Ex 3:
If a, b, c are the sides of a right angled triangle ABC right angled at C then
Sol:
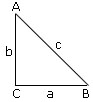
- By pythogoras theorem,
| AC2 + BC2 | = | AB2 |
| where AC | = | b |
| BC | = | a |
| AB | = | c |
| a2 + b2 | = | c2 |