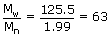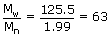Poly Dispersity Index (PDI)

Macromolecules are the "giant" molecules (polymers) formed when small organic molecules (monomers) are joined in a biological medium. Example: protein. Due to joining of many monomer units, the molecule has high molecular weight and high viscosity.

Macromolecules have a molar mass distribution due to the simplest homopolymers made of homologue chains with a different number of repeating units. They exhibit average values of two types.

i. Number average molar mass [M_n]

ii. Weight average molar mass [M_w]

The ratio of these average values give the Poly Dispersity Index (PDI) = M_w / M_n

M_n and M_w depend on the polymer chains of definite molar mass.

Calculating PDI

If the 'number average molecular weight' and 'weight average molecular weight' of a polymer are 40,000 and 60,000 respectively, then calculate the polydispersity index of the polymer. Based on the value, predict the nature of polymer.

Sol:

Given, M_w 60,000 and M_n = 40,000.

Therefore, PDI = M_w/M_n = 60,000/40,000 = 1.5 (>1). The polymer with the value (>1) have monomer units arranged in chains of different length.

M_w/M_n>1⇒ M_w>M_n ⇒ most probably it is a natural polymer.

When the PDI value is one, it indicates mono dispersity or given polymer has monomers arranged in chains of equal length.

Why does a macromolecule have several molar masses and what do these indicate ?

Sol:

Macromolecule (with exception of natural proteins and DNA) have molar mass distribution (MMD). This means that the even simplest homopolymers consists of homologue chains with a different number of repeated units. Therefore, unlike low molecular-weight components, macromolecules do not exhibit one definite molar mass. They are normally described with statistical based molar mass average values such as the molar mass averages of the number (M_n) or weight (M_w) and the polydispersity index (PDI)

Why are these averages important ?

Sol:

M_n and M_ware calculated by averaging the number or the weight of polymer chains with a defined molar mass

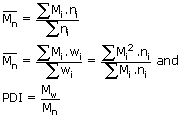
calculating M_w, M_n and PDI

Consider two polymers names A and B of each 1000 kg weight

Composition A	M_n	M_w
500 stones with 1 kg = 500 kg 2 stones with 250 kg = 500 kg Total = 1000 kgs	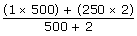=1.99	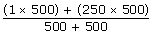=125.5
composition B 400 stones with 1 kg = 400 kg 100 stones with 6 kg = 500 kg Total = 1000 kgs	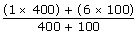=2.00	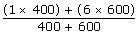=125.5

where (M_n) = number average molecular weight

(M_w) = weight average molecular weight

The polydispersity index (PDI) for A and B is therefore

PDI =