permu_comb

Ex 1:

8 – digit numbers are formed using the digits 1, 1, 2, 2, 2, 3, 4, 4. The number of such numbers in which the odd digits do no occupy odd places, is

Sol:

In 8 digit numbers, 4 places are odd places.
Also, in the given 8 digits, there are three odd digits 1, 1 and 3.
No.of ways three odd digits arranged at four even pieces =
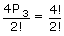
No.of ways the remaining five digits 2, 2, 2, 4 and 4 arranged at remaining five places =
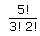
Hence, required number of 8 digits number =

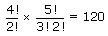
Ex 2:

Consider word ASSASSINATION, find number of ways of arranging the letters.

(i) Number of words using all.

(ii) If no two vowels are together.

(iii) If all S are separated.

(iv) Atleast one S is separated from rest of the S's.

(v) Vowels are in the same order.

(vi) Relative position of vowels and consonant remain same.

Sol:

(i) ASSASSINATION contains four S, three A, two N and two I.
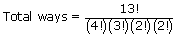
(ii) We have six vowels as A, A, A, I, I, O and seven consonants as S, S, S, S, N, T, N
| S | S | S | S | N | T | N |
ix vowels in 8 gap's
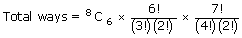
(iii) | A | A | I | N | A | T | I | O | N |
Out of 10 gaps select 4
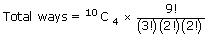
(iv) Total – all four S together
⇒ Consider 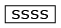as one string.
(v)
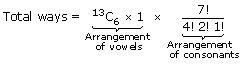
(vi)

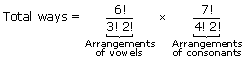
Ex 3:

Four faces of a tetrahedral dice are marked with 2, 3, 4, 5. The lowest face being considered as the outcome. In how many way a total of 30 can occur in 7 throws.

Sol:

7 throws outcome whose sum is equal to 30 can be obtained in following way.

Category	Number of ways
5, 5, 5, 5, 5, 2, 3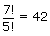
5, 5, 5, 5, 4, 4, 2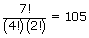
5, 5, 5, 5, 4, 3, 3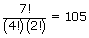
5, 5, 5, 4, 4, 4, 3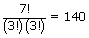
5, 5, 4, 4, 4, 4, 4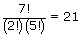

Total ways = 42 + 105 + 105 + 140 + 21 = 413.

Ex 4:

Find the number of all 6 digit numbers such that all the digits of each number are selected from the set {1, 2, 3, 4, 5} and any digit that appears in the number appears at least twice.

Sol:

Cases	No.of ways of selection	No.of ways of arrangements	Total
All alike	⁵C₁	⁵C₁ × 1	5
4 alike + 2 other alike	⁵C₂ × 2!	⁵C₂ × 2 ×	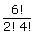300
3 alike + 3 other alike	⁵C₂	⁵C₂ ×	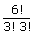200
2 alike + 2 other alike + 2 other alike	⁵C₃	⁵C₃ ×	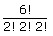900
		Total	1405