In general four normals can be drawn to an ellipse from any point, find the sum of eccentric angles of the co-normal points.

• Let the ellipse be 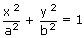.... (i)
• The normal at any point (a cos θ, b sin θ) on (i) is ax sec θ – by cosec θ = a² – b²
• If it passes through a point (x₁, y₁), then ax₁ sec θ – by₁ cosec θ = a² – b²
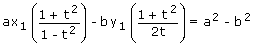• ⇒ , where t = tan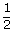θ
• ⇒ 2ax₁ (1 + t²) t – by₁ (1 + t²) (1 – t²) = 2 (a² – b²) t (1 – t²)
• ⇒ by₁ t⁴ + 2 (ax₁ + a² – b²) t³ + 2 (ax₁ – a² + b²) t – by₁ = 0 .... (ii)
• It represents 4th degree polynomial equation in t, will give in general four values of t.
• And corresponding to each value of θ we shall get one point on the ellipse, normal at which will pass through the fixed point (x₁, y₁).
• Hence from any fixed point (x₁, y₁) four normals can be drawn to the ellipse .
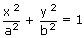• The four points on the ellipse the normals at which pass through the fixed point (x₁, y₁) are called co-normal points.
• Let the eccentric angles of these co-normal points be θ₁, θ₂, θ₃ and θ₄ and the corresponding values of t be t₁, t₂, t₃ and t₄ respectively.
• Then t₁, t₂, t₃ and t₄ are the roots of the equation (ii).
• ∴ S₁ = Σ t₁ = ,
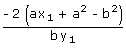• S₂ = Σ t₁ t₂ = 0,
• S₃ = Σ t₁ t₂ t₃ = 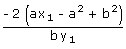and
• S₄ = t₁ t₂ t₃ t₄ =
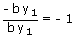
• ∴ tan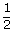(θ₁ + θ₂ + θ₃ + θ₄) = 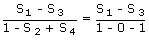which is not defined.
• Hence 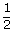(θ₁ + θ₂ + θ₃ + θ₄) = nπ + 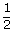π, n ∈ I
• ⇒ θ₁ + θ₂ + θ₃ + θ₄ = 2nπ + π = (2n + 1) π
• ∴ The sum of eccentric angles of the co-normal points is (2n + 1) π.

A ray emanating from the point (– 3, 0) is incident on the ellipse 16x² + 25y² = 400 at the point P with ordinate 4. Find the equation of the reflected ray after first reflection.

• For point P, y coordinate = 4.
• Given ellipse is 16x² + 25y² = 400.
• 16x² + 25(4)² = 400
• Coordinate of P is (0, 4).
• 
• 
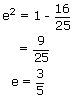
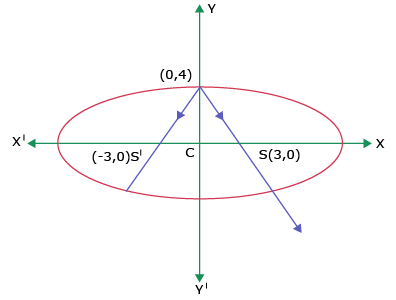
• Foci (± ae, 0) i.e, (± 3, 0).
• Equation of reflected ray (i.e, PS) is
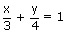• (or) 4x + 3y = 12.