Example
The graph of f(x) = ax2 + bx + c =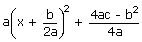 
is one of the following.
| Roots are real and not equal ⇔ Curve intersects x-axis | ||
(i) |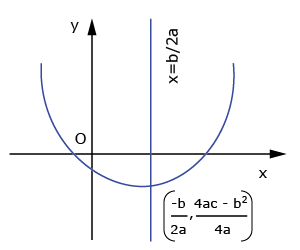
(ii) |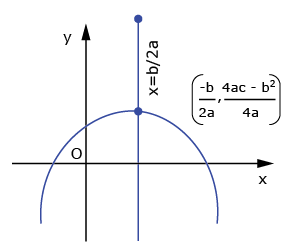
|
| Roots are real and equal ⇔ Curve touches x-axis | ||
(i) |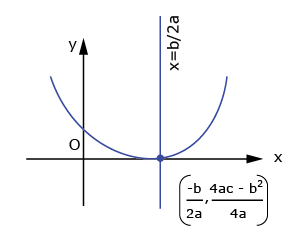
(ii) |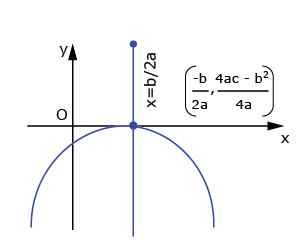
|
| Roots are non-real complex numbers ⇔ Curve doesn't meet x-axis | ||
(i) a > 0;  |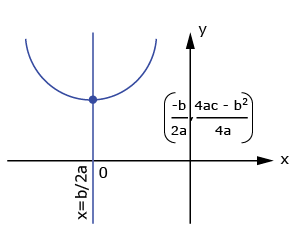
(ii) a < 0  |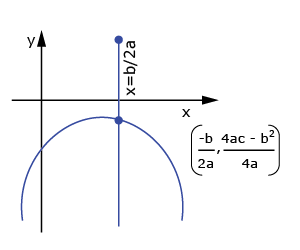
|
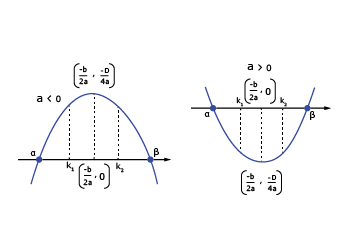
Let f(x) = ax2 bx + c, a ≠ 0 and a, b, c ∈ R, and α, β are roots of f(x) = 0. Suppose k, k1, k2 ∈ R and k1 < k2, then remember the following.
(a) Condition for a number k if both roots of f(x) = 0 are less than k.
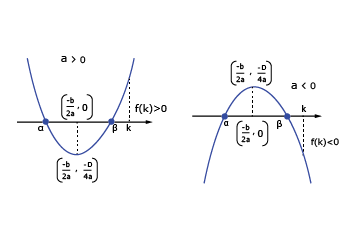
(b) Condition for a number k if both roots of f(x) = 0 are greater than k.
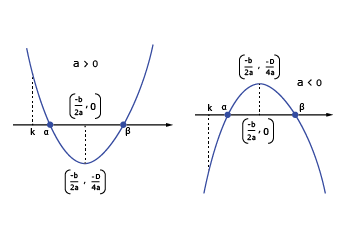
(c) Condition for k if k lies between the roots of f(x) = 0
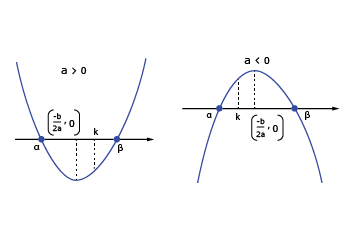
(d) Condition for the number k1 and k2 if exactly one root of f(x) = 0 lies in the interval (k1, k2)
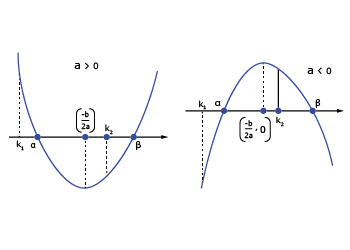
(e) Conditions for number k1 and k2 if both roots of f(x) = 0 are confined between k1 and k2
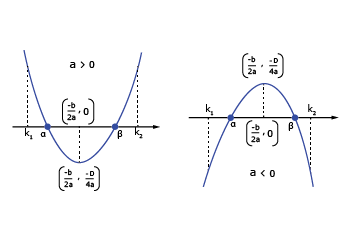
(f) Condition for number k1 and k2 if k1 and k2 lie between the roots f(x) = 0
