Examples of the law of cosines
Ex 1:
In a ΔABC, if a4 + b4+ c4 = 2c2(a2 + b2), then angle C.
Sol:
| a4 + b4 + c4 | = | 2c2(a2 + b2) |
| a4 + b4 + c4 – 2c2a2 – 2b2c2 | = | 0 |
| Adding 2a2b2 on both sides, | ||
| a4 + b4 + c4 + 2a2b2 – 2b2c2 – 2c2a2 | = | 2a2b2 |
| (a2 + b2 – c2)2 | = | (√2ab)2 |
| a2 + b2 – c2 | = | ± √2ab |
| We know that a2 + b2 – c2 | = | 2ab cos C |
| 2ab cos C | = | ± √2ab |
| cos C | = | ± (1/√2) |
| ∴ C | = | 45° (or) 135° |
Ex 2:
If D is the mid point of BC in ΔABC and AD ⊥ AC, then cos A . cos C =
Sol:
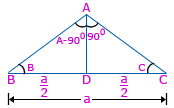
From ΔADC using sine rule,
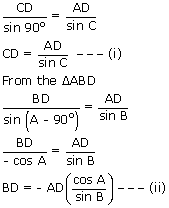
And BD = CD (∵ D is the midpoint of BC)
From (i) & (ii),
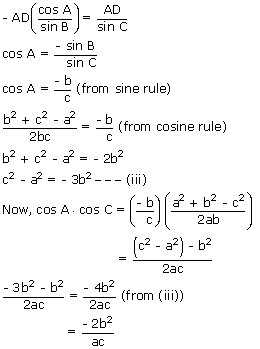
Ex 3:
The sides of a triangle are sin α, cos α and √(1 + sin α cos α) for some 0 < α < π/2. Then the greatest angle of the triangle is
Sol:
Let the given sides of a triangle are a = √(1 + sin α cos α), b = sin α, c = cos α
From cosine rule,
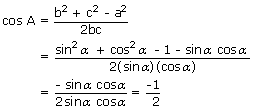
cos A = – 1/2
A = 120°
∴ Greatest angle of the triangle is 120°.