(i) The vector equation of a line passing through the point A with position vector a perpendicular to the vectors b, c is r = a + t (b × c) where 't' is a scalar.

(ii) The length of the projection of b on a vector perpendicular to a in the plane generated by a, b is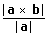

(iii) If a, b, c are the position vectors of the points A, B, C respectively, then the perpendicular distance from C to the line AB is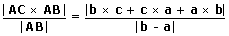

(iv) If a, b, c are triad of right-handed or left-handed system, then a × b, b × c, c × a are also triads.

(v) If a, b, c are mutually perpendicular vectors, then a × b, b × c, c × a are also mutually perpendicular vectors.

(vi) a, b, a × b are right-handed system of vectors.

(vii) a, b, b × a are left-handed system of vectors.

(viii) Vector moment of torque M of a force F acting at a point A about the point O is given by M = OA × F .

(ix) Work (W) = F.r where F = Force applied on the body, r = displacement of the body.

(x) Power (P) = F.v where v = velocity of the body.

(xi) Velocity (V) = ω × r where ω = angular velocity, r = radius vector.

(xii) Angular momentum (L) = r × p where r = position vector, p = linear momentum.

(xiii) Torque ( τ) = r × F where F = force.