Remember the following important points for the motion of freely falling bodies

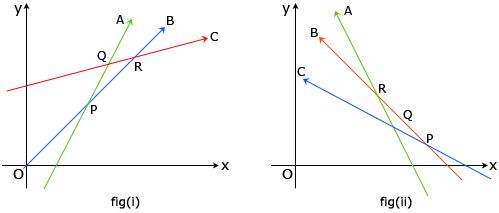
Remember the following important points for the motion of freely falling bodies

The slopes of tangents to the curve y = f(x) at the points lying in [a, b] on which f is strictly increasing are positive as shown in fig(i).
The slopes of tangents to the curve y = f(x) at the points lying in [a, b] on which f is strictly decreasing are negative as shown in fig(ii).

The slope of the tangent to the curve y = f(x) at x = c is zero if f '(c) = 0.
If f(x) is strictly increasing (strictly decreasing), then

– f(x) is strictly decreasing (strictly increasing).

Similarly if f(x) is increasing (decreasing), then

– f(x) is decreasing (increasing).

If f(x) is strictly increasing (strictly decreasing), then f is also increasing (decreasing).
If f(x) is an increasing (decreasing) function, then f(x) need not be strictly increasing (strictly decreasing).

Ex: f(x) = [x] on R is increasing.

But it is not strictly increasing.

A function f is said to be strictly increasing (strictly decreasing) and increasing (decreasing) at x = c respectively, if f(x) is strictly increasing (strictly decreasing) and increasing (decreasing) in neighborhood of c.