Derivation
Conversion from vector form to Cartesian form
We have:
 =
x
=
x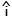 +
y
+
y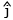 +
z
+
z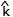 ,
,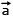 =
x1
=
x1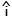 + y1
+ y1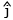 + z1
+ z1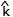 and
and =
x2
=
x2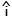 + y2
+ y2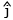 + z2
+ z2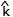 .
.Substituting these values in  =
= 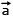 + m(
+ m( –
–
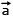 ), we
get:
), we
get:
 =
= 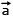 + m(
+ m( –
–
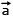 ), we
get:
), we
get:x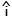 +
y
+
y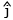 +
z
+
z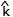 =
x1
=
x1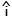 + y1
+ y1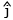 + z1
+ z1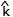 +
m[(x2 - x1)
+
m[(x2 - x1)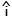 + (y2 - y1)
+ (y2 - y1)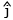 +
(z2 - z1)
+
(z2 - z1)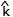 ]
]
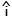 +
y
+
y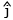 +
z
+
z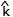 =
x1
=
x1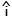 + y1
+ y1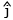 + z1
+ z1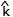 +
m[(x2 - x1)
+
m[(x2 - x1)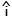 + (y2 - y1)
+ (y2 - y1)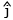 +
(z2 - z1)
+
(z2 - z1)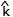 ]
]Equating the coefficients of 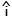 ,
, 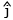 and
and 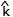 , we
get:
, we
get:
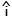 ,
, 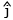 and
and 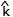 , we
get:
, we
get:x = x1 + m(x2 – x1); y = y1 +
m(y2 – y1); z = z1 + m(z2 –
z1) . . . (i)
These are parametric equations of the line. Eliminating the parameter 'm' from (i), we get:
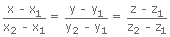 .
This is the Cartesian equation of the line.
.
This is the Cartesian equation of the line.
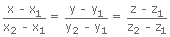 .
This is the Cartesian equation of the line.
.
This is the Cartesian equation of the line.