Theorem
If P(x, y) is any point on the ellipse whose foci are S and S', then SP +
S'P is constant.
Proof:
The equation of the ellipse is given as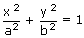 
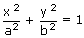(a > b) ...... (1)
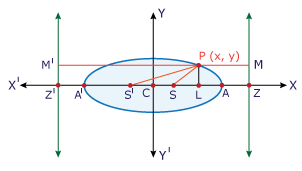
(a > b) ...... (1) Let S, S' be the foci and ZM, Z'M' be the corresponding directrices.
Join SP and S'P. Draw PL perpendicular to X-axis and M'MP perpendicular to the two directrices.
By the definition of the ellipse SP = ePM = e(LZ).
| ∴ SP | = | e(CZ – CL) |
| = |  |
|
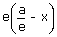| ∴ SP | = | a – xe |
| S'P | = | ePM' = e(LZ') |
| = | e(CL + CZ') | |
| = |  |
|
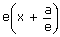| = | a + xe | |
| ∴ SP + S'P | = | a – xe + a + xe |
| ∴ SP + S'P | = | 2a(constant) = Length of the major axis. |