Examples
Ex1:
Let f: (–1, 1) → R be a
differentiable function with f(0) = –1 and
f '(0) = 1.
Let
g(x) = [f(2f(x) + 2)]2. Then find g'(0).
Sol:
| Given g(x) | = | [f(2 f(x) + 2)]2 |
| ⇒ g'(x) | = | 2 f(2 f(x) + 2)).f '(2 f(x) + 2).2f '(x) |
| Substituting x | = | 0, |
| ⇒ g'(0) | = | 2f(2 f(0) + 2)).f '(2f(0) + 2).2f '(0) |
| = | 2f(0).f '(0).2f '(0) (∵ f(0) = –1 and f '(0) = 1) | |
| = | 2(–1)(1).2(1) = – 4 |
Ex2:
Show that the function y = e–|x|
is continuous and not differentiable at x = 0.
let f(x) = 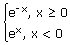
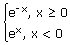
Sol:
Clearly, f(x) is continuous and differentiable for all non-zero x.
Now 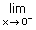 f(x) f(x) |
= |  ex = 1 ex = 1 |
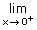 f(x) f(x) |
= |  e–x = 1 e–x = 1 |
Also f(0) = e0 = 1
So, f(x) is continuous for all
x.
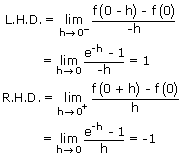
So, f(x) is not differentiable at x = 0.
Hence f(x) = e–|x| is continuous everywhere but not differentiable at x =
0.
Ex3:
Let f(x) = 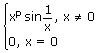
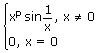
f(x) is continuous but not differentiable at x =
0. Find 'p'.
Sol:
Given f(x) = 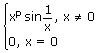
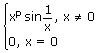
At x = 0, f(x) is a continuous function
∴  f(x) = f(0) = 0
f(x) = f(0) = 0
 f(x) = f(0) = 0
f(x) = f(0) = 0 ⇒  xp
xp 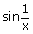 = 0
= 0
⇒ p > 0
 xp
xp 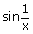 = 0
= 0 f(x) is differentiable at x = 0, if 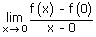 exists.
exists.
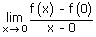 exists.
exists. ⇒ 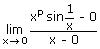 exists
exists
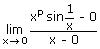 exists
exists ⇒ 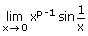 exists
exists
⇒ p – 1 > 0 or p > 1
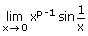 exists
exists If p ≤ 1, then  xp – 1
xp – 1 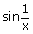 does not exist
does not exist
and f(x) is not differentiable at x = 0.
 xp – 1
xp – 1 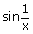 does not exist
does not exist ∴ For 0 < p ≤ 1, f(x) is a continuous function at x=0 but not differentiable.