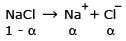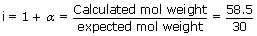Introduction of the Van't Hoff factor modifies the equations for the colligative properties as follows :
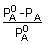 =
iXB
=
iXB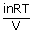 ; π = iCRT
; π = iCRTDegree of dissociation(αd) :
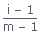 ; m =
Number of particles in solution
; m =
Number of particles in solutionDegree of association (αa) :
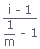 ; m = Number of particles in solution
; m = Number of particles in solutionNernst Distribution law :
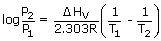
Ostwald's dilution law :
Application of Ostwald's dilution law
Based on the osmatic pressure, the solutions are classified into three major types, isotonic, hypertonic and hypotonic solutions.
i. Isotonic solutions :
Example:Solutions of urea and glucose (that do not dissociate in water); have same concentration (c1 = c2) besides osmotic pressure.
Note: Recall the relation among osmotic pressure and concentration (in molarity) as given below.

ii. Hypertonic and hypotonic solutions
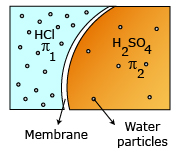
Example: Mixture of 1 N H2SO4 and 1 N HCl having osmotic pressures π1 and π2 respectively. Ionization of H2SO4:
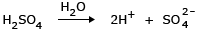
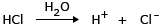
In certain solvent, phenol dimerises to the extent of 60%. Its observed molecular mass in the solvent should be
Sol:
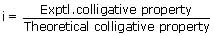
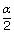
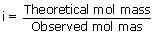
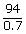
A solution containing 8.6 g urea in one litre was found to be isotonic with a 5% (wt./vol.) solution of an organic non – volatile solute. The molecular weight of latter is
Sol:
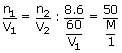
Osmotic pressure of blood is 7.55 atm at 310 K. An aqueous solution of glucose that will be isotonic with blood is...........wt/vol
Sol:
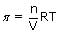
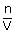 × 0.0821 × 310
× 0.0821 × 310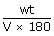 × 0.0821 × 310
× 0.0821 × 310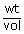 = 54.1 g/lt = 5.41%M
= 54.1 g/lt = 5.41%MThe relationship between the values of osmotic pressures of 0.1 M solutions of KN03(P1) and CH3COOH (P2) is
Sol:
∴ P1 > P2
The mol. weight of NaCl determined by studying freezing point depression of its 0.5% aqueous solution is 30. The apparent degree of dissociation of NaCl is
Sol: