EXAMPLES
Ex 1:
The base of a triangular field is three times its height. If the cost of cultivating the field at Rs. 2800 per hectare is Rs. 37800. Find its base and height.
Sol:
Total cost of cultivating field = Rs. 37800.
Rate of cultivating the field = Rs. 2800 per hectare.

Let the height of the field be x m.
Then, its base = 3x m.

Hence, height of the field = 300 m and its base = (3 × 300) m = 900 m.
Ex 2:
Triangle ABC is right–angled at A. AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm. Find the area of ΔABC. Also, find the length of AD.
Sol:

We have,
AB = 5 cm, AC = 12 cm and ∠BAC = 90°
| ∴ Area of ΔABC | = | 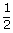 (AB ⨯ AC) (AB ⨯ AC) |
| ⇒ Area of ΔABC | = | 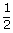 ⨯ 5 ⨯ 12 cm2 ⨯ 5 ⨯ 12 cm2 |
| ⇒ Area of ΔABC | = | 30 cm2 |
| Area of ΔABC | = | 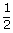 (BC ⨯ AD) (BC ⨯ AD) |
| ⇒ 30 | = | 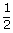 ⨯ 13 ⨯ AD ⨯ 13 ⨯ AD |
| ⇒ AD | = |  |
| = |  cm cm |
Ex 3:
A diagonal of a quadrilateral is 30 cm in length of perpendiculars to it from the opposite vertices are 6.8 cm and 9.6 cm. Find the area of the quadrilateral.
Sol:
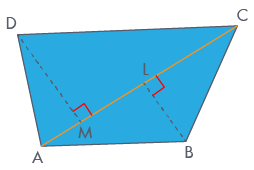
Let ABCD be the given quadrilateral and let AC it's diagonal such that AC = 30 cm.
Let BL ⊥ AC and DM ⊥ AC
Then, BL = 6.8 cm and DM = 9.6 cm
Parallelogram ABCD has one of its interior angles as 90°. Therefore, it is a rectangle.
| Area of the quad. ABCD | = | (Area of ΔABC) + (Area of ΔDAC) |
| = | 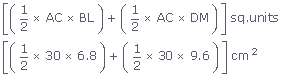 |
|
| = | (102 + 144) cm2 | |
| = | 246 cm2 |
Hence, the area of the given quadrilateral is 246 cm2.
Ex 4:
Prove that cyclic parallelogram is a rectangle.
Sol:
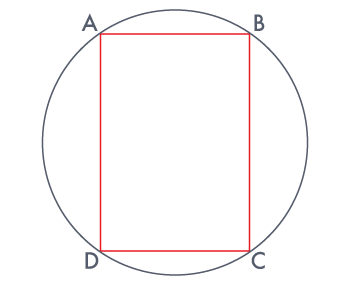
Let ABCD be a cyclic parallelogram.
∠A + ∠C = 180° (opposite angles of a cyclic quadrilateral) ...... (i)
We know that opposite angles of a parallelogram are equal.
∠A = ∠C and ∠B = ∠D
From eq. (i)
∠A + ∠C = 180°
∠A + ∠A = 180°
2∠A = 180°
∠A = 90°
Parallelogram ABCD has one of its interior angles as 90°. Therefore, it is a rectangle.
Ex 5:
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Sol:
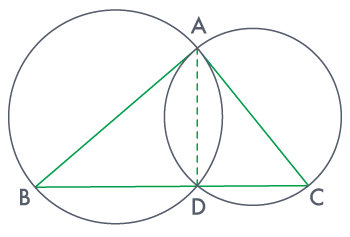
Two circles are drawn with sides AB and AC of the triangle ΔABC as diameters. Both these circles intersect each other at D.
Since, AC and AB are the diameters of the two circles.
∠ADB = 90° .... (i)
∠ADC = 90° ..... (ii)
(Angle in the semi-circle)
On adding eq (i) and (ii)
∠ADB + ∠ADC = 180°
∠BDC = 180°
Therefore, BDC is a line. That is D lies on the line segment BC.