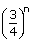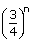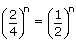Addition theorem examples

Ex 1:

Experiment : Throwing two dice for which N = 36.

Event A = getting '5' on face of first die

Event B = getting '6' on face of second die

P(A ∪ B) = Probability of getting 5 on first die or 6 on second die.

A ∪ B = {(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (1, 6), (2, 6), (3, 6), (4, 6), (6, 6)}

Note that (5, 6) should be considered only once.

⇒ n(A ∪ B) = 11

∴ P(A ∪ B) =

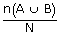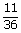.... (i)

A = {(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}

⇒ n(A) = 6

∴ P(A) =

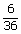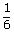
B = {(1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 6)}

⇒n(B) = 6

∴ P(B) =

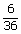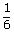
A ∩ B = {(5, 6)}

⇒ n(A ∩ B) = 1

∴ P(A ∩ B) =

Now P(A) + P(B) – P(A ∩ B) =

–

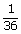
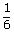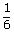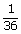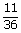.... (ii)

We see (i) and (ii) are equal.

⇒ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

Ex 2:

If P(A ∪ B) = 0.65 and P(A ∩ B) = 0.15, find

i) P(A) + P(B) and

ii) P(A) + P(B)

Sol:

i) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

0.65 = P(A) + P(B) – 0.15

⇒ P(A) + P(B) = 0.80

ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)

We know P(A) = 1 – P(A) and P(B) = 1 – P(B)

Substituting

P(A ∪ B) = 1 – P(A) + 1 – P(B) – P(A ∩ B)

⇒ P(A) + P(B)	=	2 – P(A ∪ B) – (A ∩ B)
	=	2 – 0.65 – 0.15
	=	1.2

But how come the probability is greater than 1 ?

Because it is the sum of probabilities of two events not occurring !

Ex 3:

A number is chosen from the first 100 natural numbers. Find the probability that it is a number of 4 or 6

Sol:

Given that one number is selected from first 100 natural numbers, n(S) = 100,

Let A be the event of selecting a number which is multiple of 4

Here A = {4, 8, 12 . . . . ., 100}

⇒ n(A) = 25;

Let B be the event of selecting a number which is multiple of 6;

B = {6, 12, 18, . . . . , 96}

⇒ n(B) = 16;

Here A, B are not exlcusive

(A ⋂ B) is the event of selecting a number which is a multiple of 4 and 6 i.e., it is a multiple of 12.

A ⋂ B = {12, 24, . . . . . , 96}

⇒ n(A ⋂ B) = 8;

P(A ⋃ B)	=	P(A) + P(B) – P(A ⋂ B)
	=
	=

Ex 4:

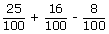
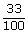
Three number are chosen at random from {1, 2, 3, . . . . , 10}. The probability that minimum of chosen number is 3 or maximum is 7, is

Sol:

A → Minimum is 3, B → Maximum is 7,

P(A ⋃ B)	=	P(A) + P(B) – P(A ⋂ B)
	=
	=

Ex 5:

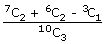
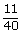
A and B are seeking admission into IIT. If the probability for A to be selected is 0.5 and that of both to be selected is 0.3. Is it possible that, the probability of B to be selected is 0.9 ?

Sol:

Given P(A) = 0.5; P(A ⋂ B) = 0.3

We know for any event A, 0 ≤ P(A) ≤ 1

So, 0 ≤ P(A ⋃ B) ≤ 1

Now by addition theorem,

P(A ⋃ B)	=	P(A) + P(B) – P(A ⋂ B)
⇒ P(B)	=	P(A ⋃ B) – P(A) + P(A ⋂ B)
	=	P(A ⋃ B) – 0.5 + 0.3
	≤	1 – 0.2
	=	0.8

P(B) ≤ 0.8 So, P(B) can not be equal to 0.9

Ex 6:

If A, B, C are mutually exclusive and exhaustive event such that P(B) = 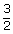P(A) and P(C) = 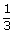P(B) Find odds in favour of (A ⋃ B)

Sol:

Since A, B, C are mutually exclusive and exhaustive

P(A) + P(B) + P(C) = P(A ⋃ B ⋃ C) = P(S) = 1

But given, 2P(B) = 3P(A) and P(B) = 3P(C)

So, 3P(A) = 2P(B) = 6P(C)

P(A) =

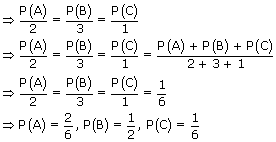
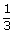; P(B) =

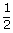; P(C) =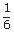

Since A, B are exclusive,

P(A ⋃ B) = P(A) + P(B) =

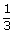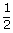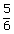
Odds in favour of (A ⋃ B) are P(A ⋃ B) : P(A ⋃ B) = 5 ∶ 1

Ex 7:

A is a set containing n elements. A subset P of A is chosen at random . The set A is reconstructed by replacing the elements of the subset of P, a subset Q of A is again chosen at random.

Find the probability that

(i) P ⋂ Q = ϕ

(ii) P ⋃ Q = A

(iii) P ⋃ Q = A and P ⋂ Q = ϕ

Sol:

Let A = {a₁, a₂, a₃, . . . . . , a_n}

For each a_k(1 ≤ k ≤ n) we have following 4 choices

(i) a_k ∈ P and a_k ∈ Q

(ii) a_k ∈ P and a_k ∉ Q

(iii) a_k ∉ P and a_k ∈ Q

(iv) a_k ∉ P and a_k ∉ Q

The total number of ways choosing the subset P and Q is 4ⁿ

(i) For the event P ⋂ Q = ϕ, out of the above 4 choices (i) choice is not favourable. So, the number of favourables for the event P ⋂ Q = ϕ is 3ⁿ required probability =

(ii) Out of 4 choices (iv) is not favourable to the ocurence of the event P ⋃ Q = A; The number of favourable ways to the occurrence of P ⋃ Q = A is 3ⁿ probability =

(iii) Out of the 4 choices (i) and (iv) are not favourables for the occurrence of event P ⋃ Q = A and P ⋂ Q = φ The number of favourable is 2ⁿ Probability =