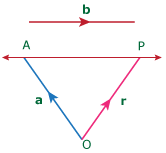
(I) The vector equation of the straight line passing through the point A (a) and parallel to the vector b is
r = a + t b, t ∈ R
Proof:
Let OP = r be any point on the line passing through OA = a.
Let b be any vector parallel to AP.
∴ AP and b are collinear vectors.
∴ AP = t b, t ∈ R (by the definition of collinear vectors)
⇒ OP – OA = t b
⇒ OP = OA + t b
∴ r = a + t b, t ∈ R
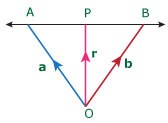
II) The vector equation of the line passing through the points A (a) and B (b) is
r = (1 – t) a + t b, t ∈ R.
Proof:
Let OP = r be point of the line passing through the points OA = a and OB = b
⇔ AP and AB are collinear vectors.
⇔ AP = t AB, t ∈ R
⇔ OP – OA = t (OB – OA)
⇔ OP = OA + t OB – t OA
⇔ OP = (1 – t) OA + t OB
⇔ r = (1 – t) a + t b, t ∈ R
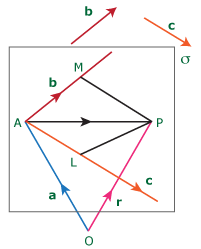
(III) The vector equation of the plane passing through the point A (a) and parallel to the vectors b and c is
r = a + t b + s c, t, s ∈ R
Proof :
Let OP = r be a point on the plane passing through the points OA = a, and parallel to the vectors b and c as shown in figure.
In a plane, through the point A, draw lines parallel to the vectors b and c with line segment AP as diagonal.
Complete the parallelogram ALPM in the a plane.
∴ A L = s c, s ∈ R and AM = t b, t ∈ R
| Now, AP | = | AL + LP |
| = | AL + AM (∵ AM = LP) | |
| OP – OA | = | sc + t b |
| OP | = | OA + t b + s c |
| r | = | a + t b + s c where t, s ∈ R. |
(IV) The vector equation of the plane passing through the points A(a), B(b) and parallel to the vector c is
r = (1 – t) a + t b + s c where t, s ∈ R
Proof:
We know that "The vector equation of the plane passing through the point A(a) and parallel to the vector b and c is
r = a + t b + s c where t, s ∈ R"
Replacing the vector b with AB, the equation of the plane is
r = a + t AB + s c
r = a + t (OB – OA) + sc
r = a + t b – t a + sc (∵ OA = a, OB = b)
∴ r = (1 – t)a + t b + s c
(V) The vector equation of the plane passing through three non-collinear points A(a), B(b), and C(c) is
r = (1 – t – s)a + t b + sc where t, s ∈ R
Proof:
Knowing that "The vector equation of the plane passing through the point A(a) and parallel to the vectors b and c is
r = a + t b + s c where t, s ∈ R"
Replacing the vector b with AB and c with AC, the equation of the plane is
| r | = | a + t AB + s AC |
| = | a + t (OB – OA) + s (OC – OA) | |
| = | a + t b – t a + sc –sa (∵ OA = a, OB = b, OC = c) | |
| ∴ r | = | (1 – t – s)a + t b + sc |