Examples
Ex 1:
Let A = {1, 2, 3}, B = {a, b, c}, C = {p, q, r}. If f : A → B, g : B → C are defined by
f = {(1, a), (2, c) (3, b)}, g = {(a, q), (b, r), (c, p)} then show that f – 1og – 1 = (gof) – 1
Sol:
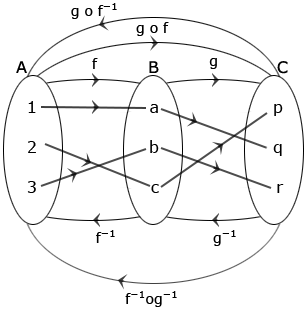
f = {(1, a), (2, c) (3, b)}, g = {(a, q), (b, r), (c, p)}
⇒ gof = {(1, q), (2, p), (3, r)}
⇒ (gof) – 1 = {(q, 1), (p, 2), (r, 3)}
g – 1 = {(q, a), (r, b), (p, c) }, f – 1 = {(a, 1), (c, 2), (b, 3)}
⇒ f – 1 og – 1= {(q, 1), (r, 3), (p, 2)}
∴ (gof) – 1 = f – 1og – 1
Ex 2:
If f : Q → Q is defined by f(x) = 5x + 4 for all x ∈ Q, show that f is a bijection and find f – 1.
Sol:
Let x1, x2 ∈ Q,
| f(x1) | = | f(x2) |
| ⇒ 5x1 + 4 | = | 5x2 + 4 |
| ⇒ x1 | = | x2 |
| ∴ f is an injection | ||
| Let y ∈ Q | ||
| Then x = (y – 4)/5 ∈ Q and | ||
f(x) = 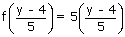 + 4 = y + 4 = y |
||
| ∴ f is a surjection and hence f is a bijection. | ||
| ∴ f – 1 : Q → Q is a bijection | ||
| We have f(x) = y ⇒ x = f– 1 (y) | ||
| 5x + 4 | = | y (∵ f(x) = 5x + 4) |
| x | = | (y – 4)/5 |
| f– 1(y) | = | (y – 4)/5 |
| ∴ f– 1 (x) | = | (x – 4)/5 for all x ∈ Q |