Pair of bisectors of angles

The equation to the pair of bisectors of angles between the pair of straight lines ax² + 2hxy + by² = 0 is h(x² – y²) = (a – b) xy

Proof:

Let ax² + 2hxy + by² = 0 represent the pair of lines

y – m₁x = 0 ----- (1)

y – m₂x = 0 ----- (2)

The combined equation of (1) & (2) is (y – m₁x) (y – m₂x) = 0

⇒ y² – (m₁ + m₂)xy + m₁m₂x² = 0

Comparing with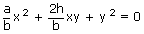

, we have

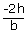m₁ + m₂ =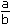

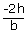; m₁m₂ =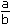

Let α, β be the angles made by the lines (1) & (2) with X-axis.

Let 'θ' be the angle (with X-axis) of the angular bisector of the lines (1) & (2).

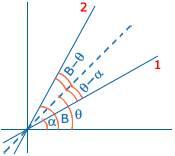
Let m₁, m₂ be the slopes of (1) & (2) respectively and m be the slope of angle bisector.

∴ m₁ = tan α; m₂ = tan β; m = tan θ

From above figure, β – θ = θ – α

⇒ 2 θ = α + β

⇒ tan 2θ = tan(α + β)

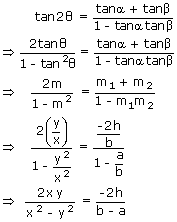
⇒ h (x² – y²) = (a – b)xy