Determinant of a matrix - Expanding by co-factors along other rows and columns
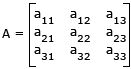
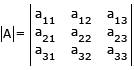
Minor of aij → Mij
Co-factor of aij → Cij
Cij = (–1)i+j.Mij
Expanding along 2nd row, we have
| |A| | = | a21.c21 + a22.c22 + a23.c23 |
| = | a21.(–1)2+1.M21 + a22.(–1)2+2.M22 + a23.(–1)2+3.M23 | |
| = | – a21 M21 + a22 M22 – a23 M23 |
In the same manner expanding along 3nd row, we have
|A| = a31 M31 – a32 M32 + a33
M33
Similarly, expanding along 1st column, we have
|A| = a11 M11 – a21 M21 + a31
M31
Expanding along 2nd column, we have
|A| = – a12 M12 + a22 M22 –
a32 M32
Expanding along 3rd column, we have
|A| = a13 M13 – a23 M23 +
a33M33
Note that the + and – signs alternate in the expansions.
Secondly, any of the above expansions is good to find the determinant of a 3 × 3 matrix.
i.e, all the expansions yield the same value of the determinant.