Indeterminate forms
In finding the values of limits, some times we obtain the following forms 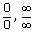 , 0 ×
∞, ∞ – ∞, 00, 1∞,
∞0 which are not defined.
, 0 ×
∞, ∞ – ∞, 00, 1∞,
∞0 which are not defined.
These forms are known as "indeterminate forms".
Some standard results on Indeterminate forms
1. Algebraic limits
i) If n is a rational number, then 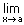
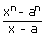 =
n.an – 1
=
n.an – 1
ii) If m, n are two real numbers, then 
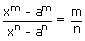 am – n
am – n
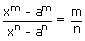 am – n
am – n
2. Trigonometric limits (where x is measured in radians)
i)  sin x = 0 sin x = 0 |
ii)  sin x = sin a, ∀ a ∈ R sin x = sin a, ∀ a ∈ R |
|
iii)  cos x = 1 cos x = 1 |
iv) 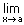 cos x = cos a, ∀ a ∈ R cos x = cos a, ∀ a ∈ R |
|
v)  tan x = 0 tan x = 0 |
vi) 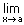 tan x = tan a,
∀ a ≠ (2n + 1) tan x = tan a,
∀ a ≠ (2n + 1)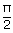 ; n ∈ Z ; n ∈ Z
|
|
vii)  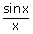 = 1
= = 1
=  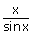 |
viii)  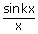 = k, ∀ k ∈ R = k, ∀ k ∈ R |
|
ix)  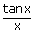 = 1
= = 1
=  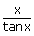 |
x) 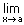  = k, ∀ k ∈ R = k, ∀ k ∈ R |
|
xi)  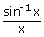 = 1
= = 1
=  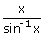 |
||
xii)  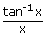 = 1
= = 1
=  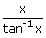 |
||
xiii) 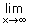 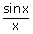 = =
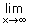 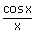 = 0 = 0
|
||
xiv) 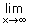 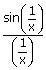 = 1 = 1 |
xv)  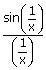 = 0 = 0 |
|
xvi)  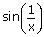 and
and  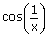 both does not exist both does not exist |
||
xvii) 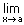 sin–1x =
sin–1a; | a | ≤ 1 sin–1x =
sin–1a; | a | ≤ 1 |
||
xviii) 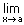 cos–1x =
cos–1a; | a | ≤ 1 cos–1x =
cos–1a; | a | ≤ 1 |
||
xix) 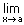 tan–1x =
tan–1a; – ∞ < a < ∞ tan–1x =
tan–1a; – ∞ < a < ∞ |
||
xx)  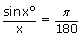 |
||
3. Exponential limits
i)  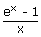 = 1 = 1 |
ii)  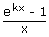 = k; k ≠ 0 = k; k ≠ 0 |
iii)  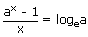 |
iv)  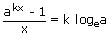 ; k ≠ 0 ; k ≠ 0 |
v)  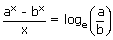 ; a, b > 0 ; a, b > 0 |
4. Miscellaneous
i) If 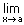 f(x)
= f(x)
= 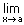 g(x) = 0, then g(x) = 0, then
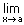
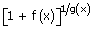
|
= | 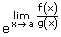 |
ii) If 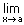 f(x) f(x) |
= | 1 and
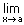 g(x) = ∞, then
g(x) = ∞, then
|
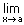
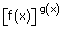
|
= | 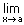 [1 + f(x) – 1]g(x)
[1 + f(x) – 1]g(x) |
| = | 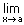 {(1 + f(x)) – 1}g(x)
{(1 + f(x)) – 1}g(x) |
|
| = | 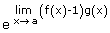 |
iii)  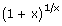 = e = e |
iv)  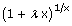 = eλ = eλ |
v) 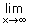 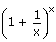 = e = e |
vi) 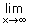 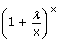 = eλ = eλ |
vii) 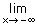 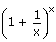 = e = e |
viii) 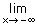 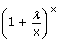 = eλ = eλ |
ix)  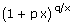 = epq = epq |
|
x) 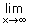 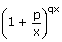 = epq = epq |
|
xi) 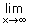 ax = ax = 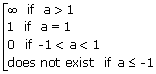 |
|
5. Logarithmic limits
i.  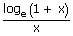 = 1 = 1 |
ii.  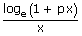 = p = p |
iii.  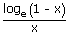 = – 1 = – 1 |
iv.  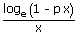 = – p = – p |
v.  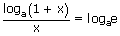 , a > 0, ≠ 1 , a > 0, ≠ 1 |