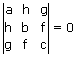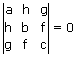Example

Find the condition that the lines ax + hy + g = 0, hx + by + f = 0, gx + fy + c = 0 to be concurrent.

Sol:

Let P(α, β) be the point of concurrence

aα + hβ + g = 0 ------ (1)

hα + bβ + f = 0 ------ (2)

gα + fβ + c = 0 ------ (3)

From (1) and (2) we get

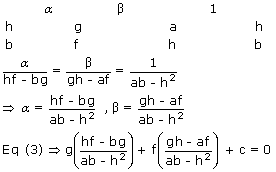
⇒ g(hf – bg) + f(gh – af) + c(ab – h²) = 0

⇒ fgh – bg² + fgh – af² + abc – ch ² = 0

⇒ abc + 2fgh – af² – bg² – ch² = 0

∴ The condition is abc + 2fgh – af² – bg² – ch² = 0.

i.e.,