To convert 180 square inches to square feet, we can follow these steps:

• 180 square inches can be written as 180 x 1 square inch.
• Since 1 square inch can be written as 1 inch x 1 inch,
• 180 square inches can be written 180 x 1 inch x 1 inch.
• Note that 1 inch can be written as 1 inch x 1 and the 1 can be written as a fraction where the numerator and the denominator are equivalent.
• Write 1 inch x 1 as 1 inch x (1 foot / 12 inches).
• This can be further simplified to read (1 inch / 1) x (1 foot / 12 x 1 inch).
• 180 square inches = 180 x 1 inch x 1 inch = 180 x 1 inch x 1 x 1 inch x 1 = (180 / 1) x (1 inch / 1) x (1 foot / 12 x 1 inch).
• Multiply the fractions. (180 x 1 inch x 1 foot x 1 inch x 1 foot) / (12 x 1 inch x 12 x 1 inch)
• Rearrange the numerator and rearrange the denominator.

  (180 x 1 inch x 1 inch x 1 foot x 1 foot) / (12 x 12 x 1 inch x 1 inch)

• Rewrite as five fractions where as many fractions as possible have an equivalent value of 1.

  (180 / 12 x 12) x (1 inch x 1 inch) x (1 inch x 1 inch) x (1 foot / 1) x (1 foot / 1)

  = 1.25 x 1 x 1 x 1 foot x 1 foot

• Note: 1 foot x 1 foot is the same as one foot squared is the same as one square foot.
• The answer is 1.25 square feet.
• Since 1 square foot is equivalent to 144 square inches, the fraction (1 square foot / 144 square inches) is equivalent to 1.

To convert 50 cubic yards to cubic feet, we can use the following steps:

• 50 cubic yards can be written as 50 x 1 cubic yard.
• Since 27 cubic feet is equivalent to 1 cubic yard, the fraction (27 cubic feet / 1 cubic yard) is equivalent to 1.
• Multiply 50 x 1 cubic yard by 1 in the equivalent form 1 = (27 cubic feet / 1 cubic yard) to obtain 50 x 1 cubic yard x (27 cubic feet / 1 cubic yard) .
• Rewrite the above expression as
  
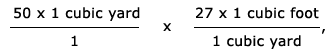
• Multiply the two fractions:
  
• Rearrange the numerator:
  
• Write the above fraction as a product of fractions so that some of the fractions have a value of 1:
  
• The answer is 1,350 cubic feet, or 1,350 feet³.

The speed limit of 80 kilometers per hour can be written as the fraction (80 kilometers / 1).

• Multiply (80 kilometers / 1) by 1 in the form : (0.621 miles / 1 kilometer)
• Multiply the two fractions:
  
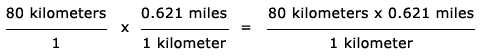
• Rearrange the numerator so that the word kilometer is to the right.
  
• At this point, you could simply cancel the kilometer in the numerator with the kilometer in the denominator. Be sure that you understand why you can do the canceling.
  
  
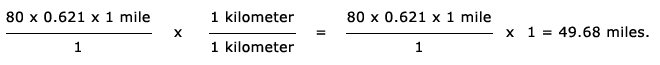
• If the speed limit is 80 kilometers per hour, you would be safe if you kept your car just under 50 miles per hour.

Method 1: Convert meters to feet to miles in one step

• Convert 100 meters to a fraction and multiply by 1 twice:
  
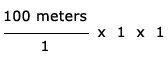
• Replace the first 1 by the fraction (3.2808 feet / 1 meter) and the second 1 by the fraction (1 mile / 5280 feet)
  
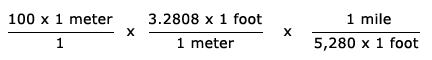
• Multiply the fractions:
  
• Look for the fractions whose values are 1 and rewrite the fraction as four fractions:
  
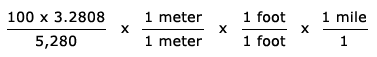
• 0.062136 x 1 x 1 x 1 mile = 0.062136 miles
• Note that his answer is not exact. It is an approximation because we rounded the answer to six places.
• When you were in high school, you probably took the original fraction and crossed out the meters and the feet. Most people do this without realizing that what they are doing is finding the fractions whose values are 1.

For the first conversion one of the conversions above may be used:

For the second conversion, centimeters to millimeters, two conversions are needed. The first converts the prefix to the base unit, and the second converts the base unit to the new prefix.