AM-GM inequality
If x and y are two non-negative numbers, then
| A.M. | = | 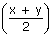 |
| G.M. | = | 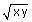 |
| We have A.M. | ≥ | G.M. |
i.e, 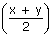 |
≥ | 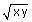 |
This is known as AM-GM inequality. |
||
Proof: |
||
| We have | ||
| (x – y)2 | ≥ | 0 |
| x2 – 2xy + y2 | ≥ | 0 |
| x2 + 2xy + y2 – 4xy | ≥ | 0 |
| (x + y)2 – 4xy | ≥ | 0 |
| (x + y)2 | ≥ | 4xy |
| x + y | ≥ | 2 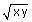 |
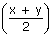 |
≥ | 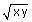 |
| A.M. | ≥ | G.M. |