Example: An electron falls through a distance of 1 m in a uniform electric field of 5 × 104 N/C. Compute its time of fall. Next calculate the time of fall for a proton, when the field is reversed.
The electron is falling through an electric field E that
is upwards.
The force that it is experiencing is ( -e).
( -E) = eE, in the downward
direction
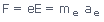
where me and
ae are the mass and acceleration of the electron.
Thus, 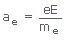
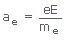
If the electron
fell through a height h, then from equations of motion,
we have h =
ute + 1/2 ate2
If the electron was
initially at rest, or gently introduced into the electric field so that u = 0, and we have
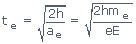
e = 1.6 × 10 -19 C,
me = 9.11 × 10 -31kg
E = 5 × 104 N/C, h = 1m
E = 5 × 104 N/C, h = 1m
Substituting the values, we get
te = 1.5
× 10 -8s
For the case of the proton, the field is downwards and it is also falling downwards.
The force that the proton is experiencing is also eE.
Solving the similar equations
for a proton falling through an electric field E = 5 × 104 N/C,
we get
tp = 6.5 × 10 -7 s (mp = 1.67 ×
10 -27 kg)
Thus the heavier proton takes more time to fall through the same distance in an
electric field.
This is contrary to what we observe when a body is "free falling"
under gravitational field.
When an object is faldivng freely, its acceleration is
9.8m/s2.
This is same for all bodies.
Therefore, a stone or a feather
dropped from the same height will reach the earth at the same time.
This does not
happen in electric field.
Let us now calculate the acceleration of the electron and
proton.
| ae | = | eE/me |
| We get ae | = | 8.7 × 1015 m/s2 |
| And ap | = | eE/mp |
| We get ap | = | 3.8 × 1013 m/s2 |
These values are enormously large when compared to gravitational
acceleration g = 9.8 m/s2.
Thus when any electric charge is falling through
an electric field, we can safely ignore gravitational effects.