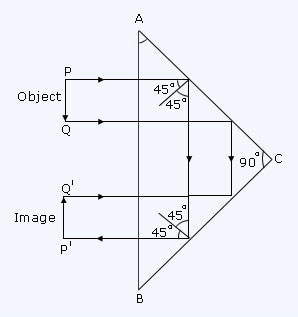
Prisms

1.

Show with the aid of a ray diagram, how a right angled isosceles prism can be used to invert the rays?

Sol:

The use of a right angled isosceles prism to invert the rays is shown in below figure.

It is based on the phenomenon of total internal reflection.

In figure, for the inverted object PQ, the upright image is P^'Q^'.

Prism

2.

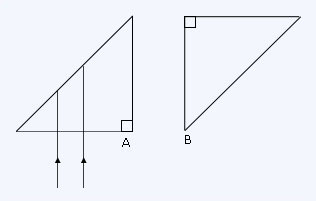
Complete the following diagram to show the rays emerging out of the prism B. State the principle used for completing the ray diagram?

Two prisms

Sol:

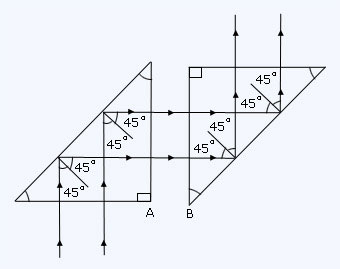
The completed ray diagram is given below in below figure.

ray diagram in prisms

The following two principles are used :

The ray of light traveling from glass, when strikes the glass–air surface at an angle of incidence greater than the critical angle (= 42° for glass–air), it suffers total internal reflection.
The ray of light falling normally on the glass–air surface, passes through it undeviated.

3.

The critical angle for glass of which the equilateral prism ABC (shown in below figure) is made, is 46°. A ray of light incident on the side AB of the prism is , refracted along DE such that the angle it makes with the side AC is 136°. Also EDB = 90°. Draw the path of the ray on the side AB (which travels along DE) and also the path, which the ray DE travels from the point E onwards ?

Sol:

The completed diagram is shown in below figure.

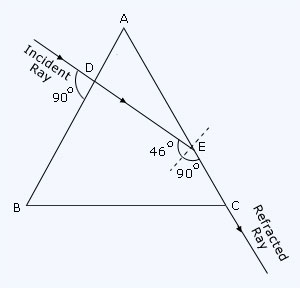
Equilateral prism ray diagram

Since the refracted ray DE is normal to the surface AB of the prism, so the incident ray at the point D should also be normal to the surface AB.

At the point E, the angle of incidence for the ray DE is 138° – 90° = 46° which is equal to the critical angle, so the ray DE is refracted at 90° i.e., along EC.