EXAMPLES
Ex 1:
A convex lens of focal length 8 cm is placed at a distance of 16 cm from a wall. How far from the lens
should an object be placed from its real image on the wall?
Sol:
Here, the real image is formed on the wall which is at a distance of 16 cm from the convex lens.
This means that the distance of the image from the convex lens or image distance will be 16 cm.
Since a real image is formed on the right side of the lens, so this image distance will be positive
| Now, Image distance, v | = | + 16 cm (A real image) |
| Object distance, u | = | ? (To be calculated) |
| Focal length, f | = | + 8 cm (It is a convex lens) |
Putting these values in the lens formula:
| 1/f | = | 1/v – 1/u |
| We get, 1/8 | = | 1/16 – 1/u |
| 1/u | = | 1/16 – 1/8 |
| 1/u | = | (1 – 2)/16 |
| 1/u | = | – 1/16 |
| So Object distance, u | = | – 16 cm |
Ex 2:
What is the focal length of a concave mirror with a radius of curvature of 14.0 cm?
Sol:
| Focal length | = | 1/2 ⨯ Radius of curvature |
| = | 1/2 ⨯ 14.0 cm | |
| = | 7.0 cm |
Ex 3:
An extended object is placed perpendicular to the principal axis of a concave
mirror with a radius of curvature of 20 cm at a distance of 15cm from the pole. Find the lateral
magnification produced.
Sol:
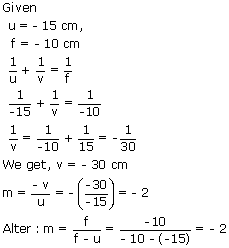
Ex 4:
A point object is placed 60cm from the pole of a concave mirror of focal length
10cm on the principal axis. Find:
(a) Position of image
(b) If the object is moved 1 mm towards the mirror along principal axis, find
the shift in image.
Sol:
(a) u = –60 cm
f = – 10cm
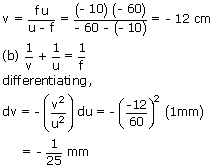
Ex 5:
A thin rod of length f/3 is placed along the principal axis of a concave mirror
of focal length f such that its image which is real and elongated just touches the rod. Calculate the
magnification
Sol:
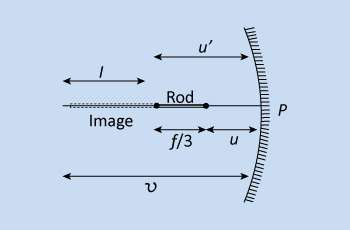
Since, the image "touches the rod", i.e., the image and object coincide.
Hence, one end of the rod should be at the centre of curvature. Given that the image is enlarged, the
rod is placed between F and C of the mirror.
Let l be the length of the image.
Then, m = l/(f/3) ⇒ l = mf/3
Also, one end of the image coincides with the object, u' = 2f.
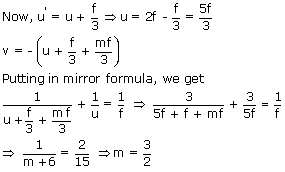
Ex 6:
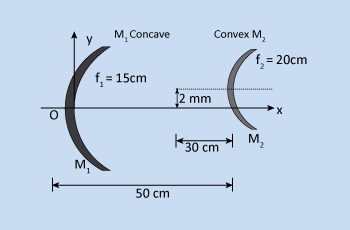
A concave and convex mirror is placed on two parallel axes as shown. Find the
coordinates of images of point object P formed after two successive reflections; first reflections at
the concave mirror and then at the convex mirror.
Sol:
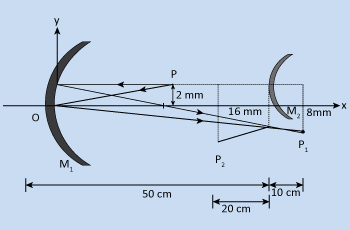
For Concave mirror M1:
u = – 20 cm, f1 = – 15 cm
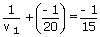
⇒ v1 = – 60 cm
Also,
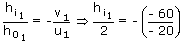
hi1 = – 6 mm.
For convex mirror M2:
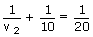
V2 = – 20 cm
for the optic axis of the convex mirror,
ho2 = 6 + 2 = 8 mm.
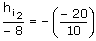
⇒ hi2 = – 16 mm.
∴ Thus, the coordinates of the image point from 'O' are (30 cm, – 14 mm).