An object is brought towards a concave mirror. How does the position and size of the image change ?

When the object is far from the concave mirror, the image is at the focus and is a diminished, inverted image. As the object is brought towards the mirror, the image shifts away from it and its size increases. When the object is at the centre of curvature of the mirror, the image is also at the centre of curvature and is of size equal to the object's size. By further bringing the object towards the mirror, the image gets magnified and moves away from the centre of curvature. The image is at infinity when the object is in the mirror's focus. Suppose the object is further moved towards the mirror. In that case, the image becomes erect and magnified and is formed behind the mirror.

The focal length of a concave mirror is 12 cm. Find the position and nature of the image formed by graphical construction when an object is placed at a distance of 6 cm from the mirror?

• Draw a vertical line MMl representing the concave mirror.
• Draw a horizontal line PC representing the principal axis.
• Take a scale, say, 1 cm = 1mm
• Mark focus F at a distance PF=12 mm (focal length = 12 cm).
• The object OA is marked at a distance PO=6 mm (distance of object = 6 cm).
• Mark centre of curvature C at a distance PC= 24 mm.
• Complete the ray diagram by taking two rays from the point A the top of the object.
• 
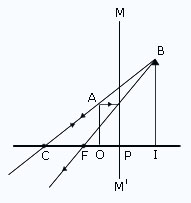
• Measure the distance PI (distance of image) = 12mm = 1.2cm
• Measure the length of object OA and the length of image IB.
• It is seen that the image is twice the size of the object.
• The image is upright, virtual and magnified.

Find the image's size, nature and position formed when an object of size 1 cm is placed at a distance of 25 cm from a concave mirror of a focal length of 20 cm?

• Here, we have been given the object distance and focal length, so first of all, we will find out the image distance which will give us the position of the image.
• (i) Position of Image
• Here, Object distance, u
  =
  – 25 cm (To the left of the mirror)
• Image distance, v
  =
  ? (To be calculated)
• And, Focal length, f
  =
  – 20 cm (It is a concave mirror)
• Now, putting these values in the mirror formula :
• 1/f
  =
  1/v + 1/u
• We get: 1/–20
  =
  1/v + 1/– 25
• (or) – 1/20
  =
  1/v – 1/25
• (or) 1/v
  =
  1/25 – 1/20
• =
  4 – 5/100
• =
  – 1/100
• So Image distance, v
  =
  –100cms
• Thus, the position of the image is 100 cm to the left side of the mirror or 100 cm in front of the mirror (the minus sign shows the left side of the mirror).
• (ii) Nature of image
• Since the image is formed in front of the concave mirror, its nature will be "Real and Inverted".
• (iii) Size of image
• To find the size of the image, we will have to calculate the magnification first.
• The magnification produced by a mirror is given by :
• m
  =
  v/u
• Here is the image distance, v
  =
  – 100cm
• Object distance, u
  =
  – 25cm
• So, m
  =
  – (–100) / (– 25) = –4
• Magnification,m
  =
  –4
• We also have another formula for magnification, which is :
• m
  =
  h₂/h₁
• Here, Magnification,m
  =
  –4 (Found above)
• Height of image,h₂
  =
  ? (To be calculated)
• Height of object,h₁
  =
  1cm (Given)
• Now, putting these values in the above magnification formula, we get:
• – 4
  =
  h₂/1
• Thus, the size of the image is 4 cm long.
• The minus sign shows that the image is formed below the principal axis.
• That is, it is a real and inverted image.