Derivation of the Formula of Refractive Index of Two Media

Find the Refractive Index of Two Media with Respect to Each Other When Their Refractive Indices With Respect to Air (or Vacuum) are Known?

Sol:

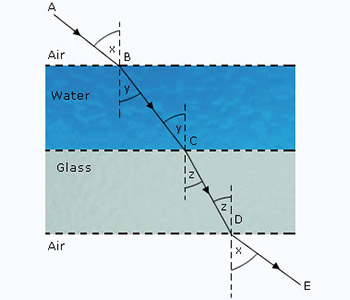
Let ABCDE be the path of a ray of light passing successively through air, water, glass and air again (see below figure). the incident ray AB finally emerges out in air in parallel direction as emergent ray DE, so. the angle of incidence x is equal to the angle of emergence x. other angles are as shown in below figure. please note that equal angles (alternate angles) are denoted by the same letters, yy and zz.

We will now write the formulae for the refractive indices corresponding to the refraction at three points B, C and D. Now :

for the refraction at point B for light going from air to water :
^aμ_w	=	sin x/sin y ----- (i)
for the refraction at point C for light going from water to glass :
^wμ_g	=	sin y⁄sin z ------ (ii)
And for the refraction at point D lor light going from glass to air :
^gμ_a	=	sin z⁄sin x ----- (iii)

Now, multiplying the left sides and the right sides of the above three equations separately, we get:

^aμ_w * ^wμ_g * ^gμ_a = sin x⁄sin y × sin y⁄sin z × sin z⁄sin x ------ (iv)

by cancelling all the factors of the right hand side, we get :

^aμ_w * ^wμ_g * ^gμ_a	=	1 ----- (v)
So, ^wμ_g	=	1^aμ_w * ^gμ_a ---- (vi)
So, We already know that: ^gμ_a	=	1^aμ_g
So, putting this values of _gμ_a in the above equation (vi), we get:
^wn_g	=	^aμ_g⁄^aμ_w
So, ^waterμ_glass	=	^airμ_glass/^airμ_water

This means that : The refractive index of glass with respect to water is equal to the ratio of refractive index of glass and refractive index of water with respect to air (or vacuum).

we can write a similar formula for the refractive index of water with respect to glass. it will be:

∴ ^waterμ_glass = ^airμ_glass⁄^airμ_water

If we consider air as medium 1, water as medium 2 and glass as medium 3, then the above formulae can be written in a general way as :

₂n₃	=	¹μ₃⁄¹μ₂
and ³μ₂	=	¹μ₂⁄¹μ₃