Derivation of the Magnification Formula for Concave Mirror
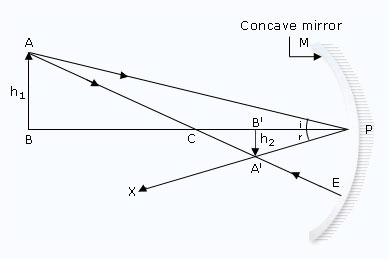
Consider an object AB placed in front of a concave mirror M beyond the centre of curvature C. To derive
the magnification formula in terms of the object distance and image distance, let us draw the
ray-diagram by using two incident rays of light:
(i) one incident ray that strikes at the pole (P) of concave mirror, and
(ii) another incident ray that passes through the centre of curvature(C) of concave mirror.
First ray:
The ray of light AP is incident at the pole P of the concave mirror. Its reflected ray PX.
The angle of reflection (r) equal to the angle of incidence (i).
Second Ray:
The second ray of light AE passing through the centre of curvature C.
It is reflected back along the same path EA.
The two reflected rays PX and EA intersect at point A',
So, A' is the real image of point A of the object.
Draw A'B' perpendicular to the principal axis.
A'B' is the complete image of the object AB.
Suppose the height of the object AB is h1,
As AB is above the principal axis, is considered positive.
Height of the image 'B' be h2
A'B' is below the principal axis, its height is considered negative.
Derivation of the magnification formula.
| In triangle ABP and A'B'P | ||
| ∠APB | = | ∠A'PB' (∵ ∠i = ∠r) |
| ∠ABP | = | ∠A'B'P (∵ both are right angles) |
| ∠PAB | = | ∠PA'B' (∵ the remaining angles) |
Thus, the triangles ABP and A'B'P are similar triangles.
∴ A'B'/AB = PB'/PB ---- (i)
Height of object, h1 = +AB
or AB = +h1 ----- (ii)
Height of image, h2 = - A'B'
or A'B' = - h2 -----(iii)
| Object distance, u | = | - PB (To the left of mirror) |
| or PB | = | - u ------(iv) |
| Image distance, ν | = | - PB' (To the left of mirror) |
| or PB' | = | - ν ------ (v) |
Now, substituting AB = + h1, A'B' = -h2, PB = -u and
PB' = - ν in equation (i), we get:
| - h2/h1 | = | - ν/-u |
| or - h2/h1 | = | ν/u |
| or h2/h1 | = | - ν/u |
| But, h2/h1 | = | m (Magnification) |
| So, Magnification, m | = | - ν/u |
| where v | = | Image distance |
| and u | = | Object distance |
m = h2/h1 = –v/u