Derivation of the Mirror Formula
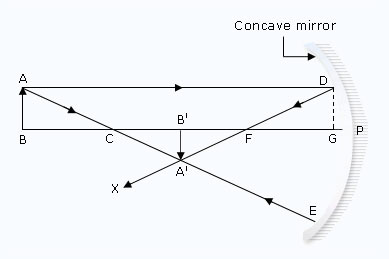
To derive the mirror formula, we will use the ray-diagram given as shown. An object AB is placed beyond
the centre of curvature (C) of a concave mirror (We could, however, place
the object at any other position also). Now, a parallel ray of light AD gets reflected from the mirror
at point D and passes through the focus F.
Another ray of light AE passing through the centre of
curvature C is reflected back along the same path EA. The two reflected rays DX and EA intersect at
point A'.
Thus, A' is the real image of point A of the object. We draw A'B'
perpendicular to the principal axis. Thus, A'B' is the real image of the object
AB. Now, from point D, let us draw DG perpendicular to the principal axis (as shown by the dotted line).
Using this
ray diagram, we will now derive the mirror formula.
Consider the triangle DGF and A'B'F (above figure). In the
triangle DGF and A'B'F. We have:
First ray:
∠DFG = ∠B'FA' (Opposite angles)
∠FGD = ∠FB'A' (Both are right angles)
∠FDG = ∠FA'B' (Remaining angles)
Thus, the triangles DGF and A'B'F are similar triangles.
∴DG/A'B' = GF/FB'
------ (i)
If we look at the above figure, we find that the triangles ABC and A'B'C
are also similar (prove it yourself),
∴AB/A'B' = CB/B'C
----- (ii)
Also, AD and BP are parallel lines:
∴ AB = DG
Now, by writing DG in place of AB in equation (ii), we get:
∴ DG/A'B' = CB/B'C
---- (iii)
If we look at equations (i) and (iii), we find that their left-hand sides are equal, so their
right-hand sides should also be equal. So, comparing equations (i) and (iii), we get:
∴ GF/FB' = CB/B'C ---- (iv)
It is clear from the figure that the distance GF is a less than the distance PF.
We will make an assumption here that the concave mirror has a very small aperture (or size) as compared
to its
radius of curvature. The point G will be very close to the pole P and we can say that GF = PF. So, by
writing PF in place of GF in the above equation, we get :
∴ PF/FB' = CB/B'C ----- (v)
From the above figure, we find that:
| (i)FB' | = | PB' − PF |
| (ii)CB | = | PB − PC and |
| (iii)B'C | = | PC − PB' |
Putting these values of FB', CB and B'C in equation (v) we get:
∴ PF/(PB' - PF) = (PB - PC)/(PC - PB') -----
(vi)
PF is the focal length and PC is the radius of curvature of the mirror. We know that the focal length
is equal to half the radius of curvature. That is :
∴ PF = PC/2
or PC = 2PF
So, by writing 2PF in place of PC in equation (vi), we get :
∴ PF/(PB' - PF) = (PB - 2PF)/(2PF - PB')
------ (vii)
The distance of an object from a mirror is called object distance and it is denoted by the
letter 'u'. The distance of the image from a mirror is called 'image distance' and denoted by the letter
'v'. And the focal length of a mirror is denoted by the
letter 'f'. We will now write down the distances PF, PB' and PB (which occur in equation
vii), in
terms of u, v and f.
(i) The object AB is to the left of the mirror, so according to the new cartesian sign
conventions, the object distance PB will have a minus sign. Thus :
Object distance, u = -PB
or PB = -u
(ii) The image A'B' is also on the left side of the
mirror, so the image distance PB' will also have a minus sign. Thus :
Image distance, v = -PB'
or PB' = -v
(iii) Similarly, the focal length PF of the concave mirror is to be measured to the left
side from the pole of the mirror, so it will also have a minus sign. Thus:
| Focal length, f | = | -PF |
| or PF | = | -f |
| Now, by putting PF | = | -f, |
| PB' | = | -v |
| and PB | = | -u in equation (vii), we get: |
| ∴ (-f/-v) - (-f) | = | [-u - 2(-f)]/[2(-f) - (-v)] |
| or (-f/-v) + f | = | (-u - 2f)/(- 2f + v) |
| or - f (-2f + v) | = | (- v + f) (- u + 2f) |
| or (2f2 - fv) | = | vu - 2v - fu + 2f2 |
| Cancelling 2f2 from both sides and remaining the equation, we get: | ||
| fu (2vf - vf) | = | vu |
| or fu + vf | = | vu |
| Now, dividing both sides by uvf, we get: | ||
| or fu/uvfvf/uνf | = | vu/uvf |
| or 1/v + 1/u | = | 1/f |
| where, v | = | distance of the image from the mirror |
| u | = | distance of the object from the mirror |
| and f | = | the focal length of the mirror. |
This is known as the mirror formula. It gives the relation between the image distance, object distance
and the focal length of a spherical mirror (concave mirror or convex mirror).