Relationship between focal length and radius of curvature

The focal length of a spherical mirror is equal to half of its radius of curvature

{f = 1/2 R}

Proof:

In below figure 1 and 2, a ray of light BP^' travelling parallel to the principal axis PC is incident on a spherical mirror PP^'. After reflection, it goes along P^'R, through the focus F, P is the pole and F is the focus of the mirror. The distance PF is equal to the focal length f. C is the centre of curvature. The distance PC is equal to the radius of curvature R of the mirror. P^'C is the normal to the mirror at the point of incidence P^'

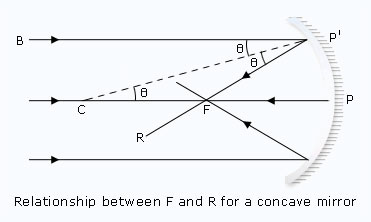
For a concave mirror:

In figure,

∠BP^'C	=	∠P^'CF (alternate angles)
and ∠BP^'C	=	∠P^'F (law of reflection, ∠i = ∠r)
Hence ∠P^'CF	=	∠CP^'F
∴ ΔFP^'C is isosceles.
Hence, P^'F	=	FC

If the aperture of the mirror is small, the point P^' is very close to the point P,

then P^'F	=	PF
∴ PF	=	FC
	=	1/2 PC
or f	=	1/2 R

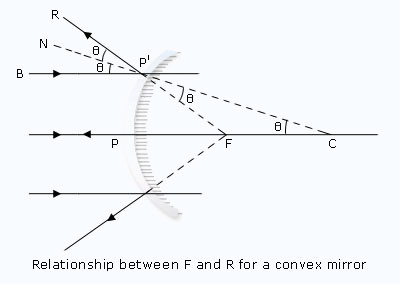
For a convex mirror:

In figure,

∠BP^'N	=	∠FCP^' (corresponding angles)
∠BP^'N	=	∠NP^'R (law of reflection, ∠i = ∠r)
and ∠NP^'R	=	∠CP^'F (vertically opposite angles)
Hence ∠FCP^'	=	∠CP^'F
∴ ΔFP^'C is isosceles.
Hence, P^'F	=	FC

If the aperture of the mirror is small, the point P' is very close to the point P.

Then P^'F	=	PF
∴ PF	=	FC
	=	1/2 PC
or f	=	1/2 R

Thus, for a spherical mirror {both concave and convex), the focal length is half of its radius of curvature.