Minimum height of plane mirror

Calculate the minimum height of plane mirror required for a person to see full height?

Sol:

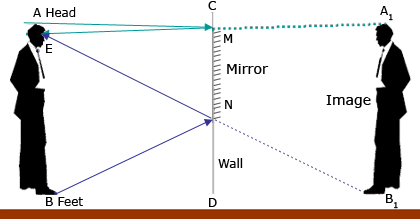
Consider a person AB, such that A represents the highest point on head, B, the lowest point on foot and E is the fixed eye level. The person will be able to see every part of his body if he can see points A and B. Let MN be the minimum length of mirror fixed on the wall, such that rays AM and BN, after reflection, reach the eye of person, thereby forming image A₁B₁, when produced backward.

In δ AEA₁, CM is parallel to AE and C is the mid–point of AA₁.

M is the mid–point of A₁E.

Similarly, in δ BEB₁ ND is parallel to BE and D is the mid–point of BB₁,

N is the mid–point of B₁E.

Now in δ A₁B₁E, M is mid–point of A₁E and N is mid–point of B₁E.

MN is parallel to and half of A₁B₁.

But A₁B₁ = AB

MN = 1/2 AB

Thus in order to see full length of a person, requires a plane mirror, which is half of its own height. This relation is true for any distance of object from plane mirror.

Here, it must be pointed out that a person can see full length of his body, by turning his head or eyes even in a small mirror. However, the case discussed is for the fixed level of eyes.