Work–Energy–theorem
Q1
Consider a baseball catcher who applies a rightward force (say
6000 N) to a leftward-moving baseball to bring it from a high speed to a rest position
over a given distance (say 0.10 meters).
Sol
According to the work–energy theorem, the
initial energy plus the work done by the external force equals the final energy.
if the ball begins with 605 joules of energy (arbitrary value), and the catcher does
external work
Wext = F.s = 6000 N × 0.10 m × cos
180° = – 600 J
then the ball will finish with 5 joules of
mechanical energy
The final energy (5 J) is equal to the initial
energy (605 J) plus the work done by external forces (–600
J).
The positive energy implies that the ball will either keep on moving
or convert this energy into another form, maybe as heat on the catcher's hand.
Q2
Consider a car, which is skidding from a high speed to a lower
speed. The force of friction between the tyres and the road exerts a leftward force (say
8000 N) on the Rightward-moving car over a given distance (say 30 m).
Sol
According to the work–energy theorem, the
initial energy plus the work done by the external force equals the final energy.
Let the car begin with 320 000 joules of energy (arbitrary value).
The friction force does work.
Wext = F.S = 8000 N × 30 m × cos 180 =
–240,000 J
The car will finish with 80 000 joules of mechanical energy.
The final energy (80 000 J) is equal to the initial energy (320 000 J) plus the work done by
external forces (240 000 J).
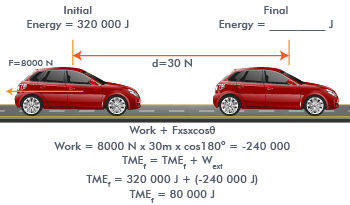
The positive energy implies that the car's speed is reduced.
Q3
Consider a cart being driven up an inclined plane at constant speed. Let the
applied force on the cart be 18 N. It is directed parallel to the incline and the
cart is displaced by 0.7 m.
Sol
According to the work–energy theorem, the
initial energy plus the work done by the external force equals the final energy.
Let the cart begins with 0 joules of energy.
Work done to pull the cart
Wext = F.s = 18 N × 0.7
m × cos 0° = 12.6 J
The cart will finish with 12.6 joules of mechanical energy
The final energy (12.6 J) is equal to the initial energy (0 J) plus the work done by external forces
(12.6 J).
The positive energy implies that the cart has more potential energy when it is at the new height.
In each of these examples, an external force does work upon an object over a given distance to change
the total mechanical energy of the object.
If the external force does positive work, then the object gains energy; the amount of energy
gained is equal to the work done on the object.
If the external force does negative work, then the object loses energy; the amount of energy
lost is equal to the work done on the object.