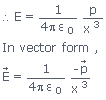Derivation
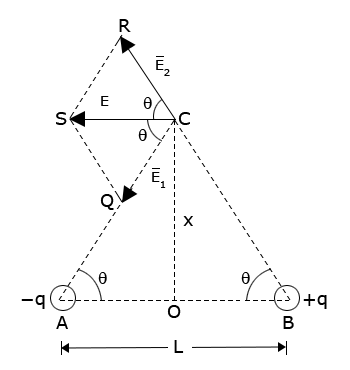
let C be a point on the equatorial line of the dipole at a distance x from the centre of the dipole (i.e. OC = x).
Let us find the electric field intensity at C due to the dipole.
Let ∠CAB = ∠CBA = θ.
Let E1 be the electric field intensity at C due to – q. then,
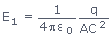
| But AC2 | = | OC2 + AO2 |
| = | x2 + (L/2) | |
| Let (L/2) | = | l, |
| then AC2 | = | x2 + l2 |
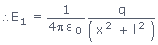
is represented both in magnitude and direction by 
If E2 is the electric field intensity at C due to + q then
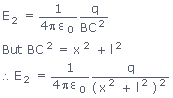
is represented both in magnitude and direction by 
.It is clear from the above equations that E1 = E2.
When the two electric fields 
and 
are resolved into rectangular components ,then it is clear that the components along
the equatorial line are equal in magnitude but in opposite directions.
But the components perpendicular to the equatorial line get added up because they act in the same direction.
So the magnitude of the resultant electric field intensity due to the two charges(i.e., due to the dipole) is given by E .
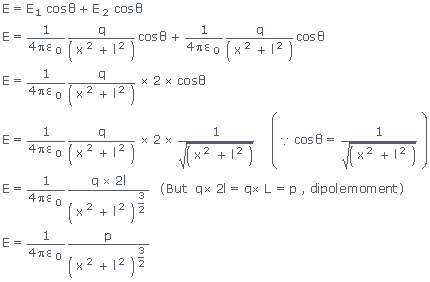
If the dipole is short enough (i.e. L<<x),
then (L/2)2 = l2 may be neglected as compared to x2
