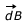 at the centre O of the coil due to current element I
at the centre O of the coil due to current element I 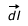 is given by
is given by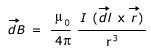
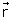 is the position vector of point O from the current element.
is the position vector of point O from the current element.The magnitude of 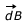 at the centre O is
at the centre O is
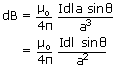
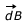 is perpendicular to the plane of the coil and is directed inwards.
is perpendicular to the plane of the coil and is directed inwards.Since each current element contributes to the magnetic field in the same direction, the total magnetic field B at the center O can be found by integrating the above equation around the loop i.e.
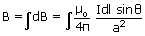
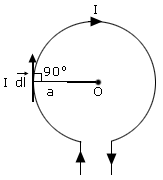
For each current element, angle between 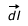 and
and
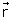 is 90°.
is 90°.
Therefore 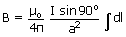
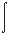 dl = Total length of the coil
dl = Total length of the coil
 a
a 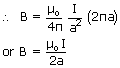
If the coil has n turns, each carrying current in the same direction, then contributions of all the turns are added up, then B = 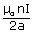
Consider a circular coil of radius a, centre O and carrying a current I in the direction shown in figure.
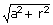
 QPO = α =
QPO = α =  RPO
RPOAccording to Biot-Savart law, the magnitude of magnetic field at P due to current element at Q is given by
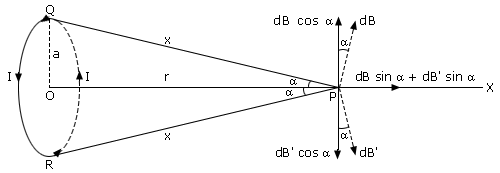
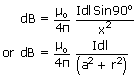
The magnetic field at P due to current element at Q is in the plane of paper and at right angles to 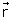 and in the direction shown.
and in the direction shown.
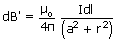
It also acts in the plane of paper and at right angle to 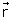 but in opposite direction to dB.
but in opposite direction to dB.
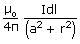
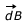 and
and
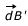 into rectangular components, it is clear that vertical components (dB cosα and dB' cos α) will be equal and opposite and thus cancel each other.
into rectangular components, it is clear that vertical components (dB cosα and dB' cos α) will be equal and opposite and thus cancel each other.
However, components along the axis of the coil (dB sin α and dB' sin α) are added and act in the direction PX.
Therefore, when we sum up the contributions of all the current elements of the coil, the perpendicular components will cancel.
 B =
B = 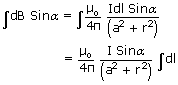
Now sin α = 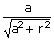 and
and 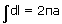
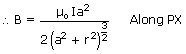
If the circular coil has n turns then,
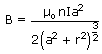 along PX
along PX