According to the first law of Thermodynamics change in internal energy is
| ΔU | = | Q – W |
| Work done by the system W | = | 164 J |
| Heat gained by the system Q | = | 77 J |
| Change in internal energy of the system ΔU | = | 77 – 164 |
| = | – 87 J | |
| This means that the internal energy of the system decreases. | ||
| Now in the case of environment | ||
| Work is done on the environment W | = | – 164 J |
| Heat is given to the system Q | = | – 77 J |
| ∴ Change in internal energy ΔU | = | – 77 + 164 |
| = | 87 J | |
This means that internal energy of the environment increases.
A gas, while expanding under isobaric conditions, does 480 J of work. The pressure of the gas is 1.6 × 105 pa, and its volume is 1.5 × 10– 3 m3. What is the final volume of the gas ? –1 for all frequencies, calculate the wave lengths corresponding to the given extreme frequencies of the range ?
| W | = | P(V2 – V1) |
| But here W | = | 480 J |
| P | = | 1.6 × 105 pa |
| V1 | = | 1.5 × 10– 3 m3 |
| ∴ Final volume V2 | = | 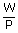 + V1 + V1 |
| = | 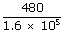 + 1.5 × 10
– 3 + 1.5 × 10
– 3 |
|
| = | 4.5 × 10– 3 m3 |
A certain gas at atmospheric pressure is compressed adiabatically so that its volume becomes half of its original volume. Find the resulting pressure. Given γ = 1.4 ?
In an adiabatic process, the relation between pressure and volume is given by PVγ = constant
| or P1V1γ | = | P2V2γ |
| Given Initial pressure P1 | = | 1 atm |
| = | 1.013 × 105 N/m2 | |
| Final volume V2 | = |  V1 V1 |
| γ | = | 1.4 |
| Putting these values in the above equation, we get | ||
| P2 | = | P1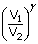 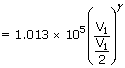 |
| = | 1.013 × 105(2)1.4 | |
| = | 2.7 × 105 N/m2 | |
Calculate the work done to isothermally compress 1g of hydrogen gas at NTP to half of its initial volume. Gas constant R = 8.31 J.mol k. Find the change in internal energy and amount of heat evolved ?
Work done in an isothermal process is
| W | = | 2.3026 RT log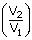 |
| For 1g of gas W | = | 2.3026 × 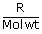 × T log × T log
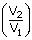 |
| Here, Mol.wt of the gas (H2) | = | 2 |
| Gas constant R | = | 8.314 J/mol k |
| Temperature T | = | 273 k (NTP conditions) |
| Initial volume, V1 | = | V |
| Final volume, V2 | = | 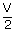 |
| ∴ W | = | 2.3026 × 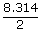 × 273 log × 273 log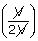 |
| = | – 786.3 J |
A cylinder contains 1 mole of oxygen at a temperature of 27° c. The cylinder is provided with a frictionless piston which maintains a constant pressure of 1 atm on the gas. The gas is heated until its temperature rise to 127° c. Calculate the work done by the gas, increase in the internal energy and the heat supplied to gas ? Cp = 7.03 cal/mol k, R = 1.99 cal/mol k
| So initial temperature T1 | = | 27 + 273 |
|
|
= | 300 k |
| Final temperature T2 | = | 127 + 273 |
|
|
= | 400 k |
| Work done in an adiabatic process is W = PdV | ||
| but PV = RT for one mole of a gas. | ||
| ∴ W | = | PdV |
|
|
= | RdT |
|
|
= | R(T2 – T1) |
| Given R | = | 1.99 cal/mol k |
|
|
= | 1.99 × 4.2 J/mol k |
|
|
= | 8.358 J/mol k |
| ∴ Work done W | = | 8.358(400 – 300) |
|
|
= | 835.8 J |
| Change in internal energy of the gas dU | = | CvdT |
| Given Cp | = | 7.03 cal/mol k |
|
|
= | 7.03 × 4.2 J/mol k |
|
|
= | 29.53 J/mol k. |
| But Cp | = | Cv = R |
| ⇒ Cv | = | Cp – R |
|
|
= | 29.53 – 8.358 |
|
|
= | 21.168 J/mol k |
| ∴ Increase in the internal energy of the gas | ||
| dV | = | CvdT |
|
|
= | 21.168(400 – 300) |
|
|
= | 2117 J |
| The amount of heat supplied to the gas is | ||
| dQ | = | CpdT for 1 mole of the gas |
|
|
= | 29.53(400 – 300) |
|
|
= | 2953 J |
| t | = | 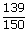 |
| ; | = | 0.275 hr |
| ; | = | 0.275 × 60 min |
| t | = | 16.4 min |
| Q | = |  mv2 mv2 |
i.e.,  mv2 mv2
|
= | 139 kcal |
| Given m | = | 60 kg |
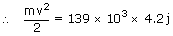 |
||
| v2 | = | (583.8 × 103 J)/30 |
| v | = | 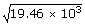 |
| v | = | 139 m/s |
| ; | = | 139 × 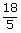 km/hr km/hr
|
| ; | = | 501 km/hr |
The speed with which the person can walk after eating the doughnut is 501 km/hr
Given data is
| Heat taken by the engine QH | = | 1.61 × 104 J |
| Work done per cycle W | = | 3700 J |
| Latent heat of combustion Lc | = | 4.6 × 104 J/g |
| (a) Thermal efficiency e | = |  |
| = | 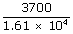 |
|
| = | .2298 × 10– 4 | |
| ; | = | 0.23 × 100 |
| e | = | 23 % |
| (b) We know that work done | = | Heat input – Heat rejected |
| ∴ Amount of heat rejected in each cycle | ||
| Qc | = | QH – W |
| ; | = | 1.61 × 104 – 3700 |
| ; | = | 12400 J |
| Heat required to burn the gasoline is given by | ||
| QH | = | mLc |
| ⇒ m | = | 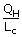 |
| ; | = | 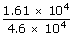 |
| ; | = | 0.35 g |
| Power output | = | 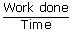 |
| ; | = | (work done) × (no of cycles) |
|
Given number of cycles per sec
|
= | 60 |
| ∴ Power output | = | (3700 J/cycle)(60 cycles/sec) |
| ; | = | 222000 W |
| ; | = | 222 kW |
A gasoline engine has a power output of 180 kw. Its thermal efficiency is 28 %. How much heat must be supplied to the engine per second and how much heat is discarded by the engine per second ?
| Given power output | = | 180 kw |
| ∴ Work done per sec | = | 180 × 103 J |
| Thermal efficiency, e | = | 28 % = 0.28 |
| ∴ Heat supplied to the engine | = |  |
| = | 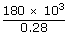 |
|
| QH | = | 642.8 × 103 J |
| Heat rejected by the engine Qc | = | QH – W |
| ; | = | 642.8 × 103 – 180 × 103 |
| ; | = | 462.8 × 103 J |
A carnot engine whose high temperature reservoir is at 620 k takes in 550 J of heat at this temperature in each cycle and gives up 335 J to the low temperature reservoir. How much work does the engine perform during each cycle and what is the temperature of low temperature reservoir ? Find the thermal efficiency of the cycle ?
| Temperature of high temperature reservoir TH | = | 620 k |
| Heat input QH | = | 550 J |
| Heat rejected Qc, to cold reservoir Qc | = | 335 J |
| work done per cycle W | = | QH – Qc |
| = | 550 – 335 | |
| = | 215 J | |
| Thermal efficiency e | = | 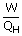 |
| ; | = | 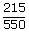 |
| ; | = | 0.39 × 100 |
| e | = | 39 % |
| But efficiency e | = | 1 – 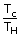 |
| Temperature of cold reservoir Tc | = | (1 – e)TH |
| ; | = | (1 – 0.39)620 |
| ; | = | 378.2 k |
A carnot heat engine has a thermal efficiency of 0.6 and temperature of its hot reservoir is 800 k. If 3000 J of heat is rejected to the cold reservoir in one cycle, what is the work output of the engine during one cycle ?
| Thermal efficiency of the carnot engine e | = | 0.6 |
| Amount of heat rejected to cold reservoir Qc | = | 3000 J |
| Temperature of hot reservoir TH | = | 800 k |
| We know that efficiency e | = | 1 – 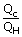 |
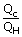 |
= | (1 – e) |
| QH | = | 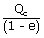 |
| QH | = | 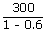 |
| QH | = | 7500 J |
| Now the amount of work done can be found from the relation | ||
| W | = | QH – Qc |
| ; | = | 7500 – 3000 |
| W | = | 4500 J |
Find the change in entropy when 1 kg of ice at 0° c is melted and converted to water at 0° c. Also find the change in entropy when 1 kg of water at 0° c is heated to 100° c. Heat of fusion of water Lf = 3.34 × 105 J/kg
| Heat needed to melt 1 kg of ice is Q | = | mLf |
| = | 1 × 3.34 × 105 J | |
| ∴ The increase in entropy Δs | = | 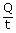 |
| = |  |
|
| = | 1.22 × 103 J/k |
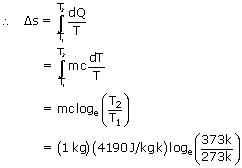 Hence the change in entropy is = 1.31 × 103 J/k
Hence the change in entropy is = 1.31 × 103 J/k