What is the average translational kinetic energy of molecules in an ideal gas at 40°c ?
Average translational KE 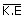 =
= 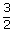 KT
KT
| K | = | Boltzmann's constant = 1.38 × 10–23 J/k |
| T | = | absolute temperature = 40 + 273 |
| = | 313 k | |
∴ 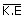
|
= | 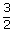 (1.38 × 10– 23)(313) (1.38 × 10– 23)(313) |
| = | 6.48 × 10–21 J |
Calculate the temperature at which rms velocity of gas molecules is double its value at 27° c, pressure of the gas remaining constant.?
| We know that Vrms | = | 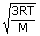
|
here 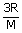
|
= | constant |
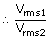
|
= | 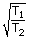
|
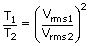
|
||
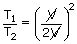
|
||
| T2 | = | 4T1 |
| = | 1200 k | |
| = | 927°c | |
Calculate the total number of degrees of freedom possessed by the molecules in one cm3 of H2 gas at NTP
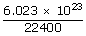 = 0.26875 × 1020
= 0.26875 × 1020| ∴ Total number of degrees of freedom of 0.26875 × 1020 molecules | = | 0.26875 × 1020 × 5 |
| = | 1.34375 × 1020 |
Find the mean free path of air molecules at STP. The diameter of O2 and N2 molecules is about 3 × 10–10 m
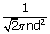
| ∴ n | = | 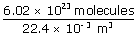
|
| = | 2.69 × 1025 molecules/m3 | |
| ∴ Mean free path λ | = | 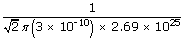
|
| λ | = | 9 × 10–8 m |
How many degrees of freedom are associated with 2g of He at NTP? Calculate the amount of heat energy required to raise the temperature of this amount from 27°c to 127°c.
 × 6.02 × 1023 = 3.01 × 1023 molecules
× 6.02 × 1023 = 3.01 × 1023 molecules| Now total degrees of freedom of 2g of He is | ||
| f | = | (Total number of molecules) × (Degrees of freedom per molecule) |
| f | = | 3.01 × 1023 × 3 |
| = | 9.03 × 1023 | |
| We know that energy associated with one degree of freedom per molecule | ||
| U | = |  KT KT |
| Energy associated with 2g of He is | ||
| U | = | (Total degrees of freedom) ×  KT KT |
| U | = | f ×  KT KT |
| U | = | 9.03 × 1023 ×  1.38 × 10
-23 × T 1.38 × 10
-23 × T |
| Energy at 27° c | = | 27 + 273 |
| = | 300 k | |
| U1 | = | 9.03 × 1023 ×  1.38 × 10
-23 × 300 1.38 × 10
-23 × 300 |
| = | 1869.2 J | |
| Energy at 127° c | = | 127 + 273 |
| = | 400k | |
| U2 | = | 9.03 × 1023 ×  1.38 × 1023 × 400 1.38 × 1023 × 400 |
| = | 2492.3 J | |
| Heat energy required to raise the temperature from 27° c to 127° c is | ||
| U2 – U1 | = | 2492.3 – 1869.2 |
| = | 623.1 J | |
The pressure of sulphur dioxide (SO2) is 2.12 × 104 pa. There are 420 moles of this gas in a volume of 50 m3. Find the translational rms speed of the SO2 molecules
Translational rms speed is related to the pressure and density of the gas by the equation
| Vrms | = | 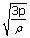
|
| ρ | = | density of the gas |
| = | 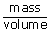
|
|
| Given volume of the gas V | = | 50 m3 |
| Molar mass of SO2 | = | 64 g/mol |
| But there are 420 moles in 50 m3 gas | ||
| ∴ Total mass m | = | 64 × 420 |
| Pressure of the gas is P | = | 2.12 × 104 pa |
| Substituting all these values, we get | ||
| Vrms | = | 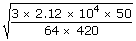
|
| = | 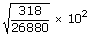
|
|
| = | 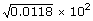
|
|
| = | 10.8 m/s | |