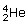Worked out example
Q.
The most abundant isotope of helium has a nucleus whose mass is 6.6447 × 10− 27 kg. For this nucleus, find
(a) the mass defect and
(b) the binding energy.
Given mass of proton = 1.672 622 × 10− 27, mass of neutron = 1.674 927 × 10− 27 ?
Sol.

(a) The helium nucleus contains Z = 2 protons and N = 4 − 2 = 2 neutrons. To obtain the mass defect Δm, we first determine the sum of the individual masses of the separated protons and neutrons.

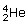Then we subtract from this sum the mass of the nucleus.

The sum of the individual masses of the nucleons is 2(1.6726 × 10− 27 kg) + 2(1.6749 × 10− 27 kg) = 6.6950 × 10− 27 kg

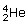This value is greater than the mass of the intact nucleus, and the mass defect is

Δm = 6.950 × 10− 27 kg − 6.6447 × 10− 27 kg = 0.0503 × 10− 27 kg

(b) According to equation of the binding energy, (Δm)c2 = 0.0503 × 10− 27 kg)(3.00 × 108 m/s)2 = 4.53 × 10− 12 J

Usually, binding energies are expressed in energy units of electron volts instead of joules (1 eV = 1.60 × 10− 19 J):

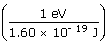Binding energy = (4.53 × 10− 12 J) = 2.83 × 107 eV = 28.3 MeV

n this result, one million electron volts is denoted by the unit MeV. The value of 28.3 MeV is more than two million times greater than the energy required to remove an orbital electron from an atom.