Two identical spherical drops of water are falling through air with a steady velocity of 20 cm/s. if the drops combine to form a single drop, what would be the terminal velocity of the single drop?
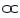 r2
r2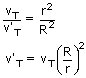
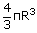
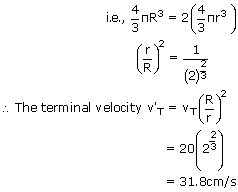
The terminal velocity of a copper ball of radius 2mm falling through a tank of oil at 200c is 6.5 cm/s. Compute the viscosity of the oil at 200c. Density of oil = 1.5 × 103 kg/m3 and density of copper = 8.9 × 103 kg/m3
| Terminal velocity vT | = | 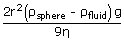
|
| So viscosity of the oil η | = | 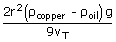
|
| Given,radius of the copper ball r | = | 2mm |
| = | 2 × 10-3m | |
| Density of the copper ball ρcopper | = | 8.9 × 103 kg/m3 |
| density of the oil ρoil | = | 1.5 × 103 kg/m3 |
| Terminal velocity vT | = | 6.5 cm/s |
| = | 6.5 × 10-2 m/s | |
| Acceleration due to gravity g | = | 9.8 m/s |
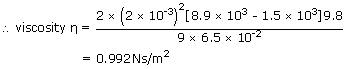
|
In Millican's oil drop experiment, what is the terminal velocity of an uncharged drop of radius 2 × 10-5 m and density 1.2 × 103 kg/m3. Take the viscosity of air at the temperature of the experiment to be 1.8 × 10-5 pas. How much is the viscous force on the drop at that speed?. Neglect the bouncy of the drop due to air.
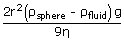
 vT vT |
= | 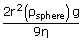
|
| Given radius of the drop | = | 2 × 10-5m |
| density of the drop | = | 1.2 × 103 kg/m3 |
| viscosity of air | = | 1.8 × 10-5 Ns/m2 |
| Acceleration due to gravity | = | 9.8 m/s2 |
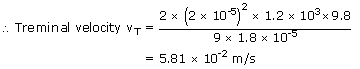
|
||
| To find the viscous force F, we use | ||
| F | = | 6π η γvT relation |
 F F |
= | 6π(1.8 × 10-5)(2 × 10-5)(5.81× 10-2) |
| Viscous force F | = | 3.94 × 10-10N |