Heron's formula
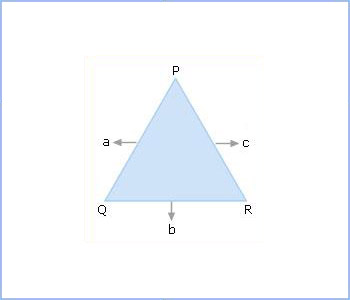
Let 'a', 'b', 'c' be the lengths of the sides of a Δ PQR.
Then, the area of Δ PQR is given as: 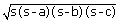 , where s = semi-perimeter of the
triangle.
, where s = semi-perimeter of the
triangle.
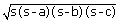 , where s = semi-perimeter of the
triangle.
, where s = semi-perimeter of the
triangle.
The above formula for calculating the area of triangle is known as Heron's formula.
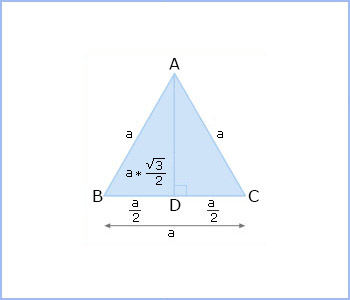
Area of an equilateral triangle
Let ABC be an equilateral triangle with side a.
Therefore, AB = BC = AC = a.
The height of an equilateral triangle is the length drawn from opposite vertex to that side.
Here, the height is given by AD = 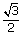 × a.
× a.
We know that, area of  le le |
= |  × base
×
height. × base
×
height. |
| = |  × BC
×
AD × BC
×
AD |
|
| = |  × a
× × a
×
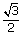 a a
|
|
| = | 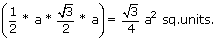 |
|
 Area of
equilateral
Δle with side 'a' Area of
equilateral
Δle with side 'a' |
= | 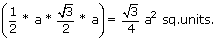 |
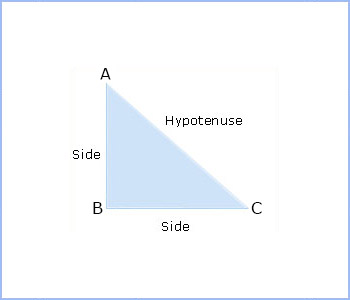
Area of a right-angled triangle
Let ABC be a right angled triangle with  B = 90°.
B = 90°.
 B = 90°.
B = 90°.
 Area of Δ ABC =
Area of Δ ABC =  × [Product of sides
containing 90°]
× [Product of sides
containing 90°]
=  × BC × AB sq. units.
× BC × AB sq. units.
 × BC × AB sq. units.
× BC × AB sq. units.Note: If ABC is a right angled triangle then
Hypotenuse2 = side2 + side2. If one side and hypotenuse is
given, we can measure the other side and we can also measure the area.

Isosceles right-angled triangle
In a right angled triangle, if base = height then that becomes an isosceles right-angled triangle.
Let ABC be an isosceles right angled triangle. Therefore,
| Area of Δ ABC | = |  ×
[Product of
sides containing 90°] ×
[Product of
sides containing 90°] |
| = |  × BC
× AB. × BC
× AB.
|
|
| = |  × AB
× AB
[ × AB
× AB
[ BC = AB] BC = AB] |
|
| = |  ×
(AB)2
sq. units. ×
(AB)2
sq. units. |